Линейный оператор

ЛЕКЦИИ ПО ДИСЦИПЛИНЕ

«ЛИНЕЙНАЯ АЛГЕБРА»

Направление 080100

«Экономика»

Очная форма обучения

Рязань 2012

Тема 9. Линейные операторы

Отображения, линейные операторы.

Структура линейного оператора (образ, ядро, ранг, дефект, основные равенства).

Матрица линейного оператора.

Матрицы линейного оператора в разных базисах.

Собственные векторы, собственные значения линейного оператора

Основные свойства собственных векторов линейного оператора.

Приведение матрицы линейного оператора к диагональному виду.

Ортогональные операторы, основные теоремы об ортогональных операторах.

Линейный оператор

В линейной алгебре часто рассматриваются соответствия, при которых векторам одного линейного пространства ставят в соответствие векторы другого (или того же) линейного пространства.

Определение 5.1. Пусть заданы два линейных пространства . Если каждому вектору 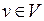поставлен в соответствие единственный вектор

,

то говорят, что в пространстве задано отображение (функция)

.

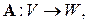
При этом вектор 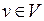называют прообразом вектора , а вектор 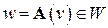– образом вектора 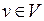. Линейные пространства называются соответственно пространством прообразов и пространством образов.

Частным случаем отображения линейных пространств является отображение пространства на себя:

.

Определение 5.2. Отображение 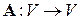, переводящее линейное пространство V в себя, называется линейным оператором (или линейным преобразованием), действующим в V, если для любых векторов и любого числа :

1) (аддитивность),

2) (однородность).

При этом запись , или называют операторной записью (или операторным равенством).

Условия 1), 2) определения 5.2 можно скомбинировать в виде одного: для любых векторов и любых чисел :

.

Отметим ряд свойств линейного оператора, непосредственно следующих из определения 5.2.

Теорема 5.1 (об образе нулевого вектора). Линейный оператор переводит нулевой вектор в нулевой вектор.

□ Имеем . ■

Приведенное свойство может рассматриваться как необходимое (но не достаточное) условие линейности оператора. Если данное свойство не выполняется для данного отображения, то это отображение не является линейным оператором.

Теорема 5.2 (об образе линейной комбинации). При линейном преобразовании 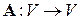образ линейной комбинации равен линейной комбинации образов, то есть если задана система векторов , то

.

Доказательство следует непосредственно из определения 5.2.

Теорема 5.3. Если система векторов линейно зависима, то система образов также линейно зависима.

□ Если система векторов линейно зависима, то существуют числа , среди которых есть хотя бы одно отличное от нуля, что

, .

Тогда, действуя оператором 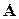на обе части этого равенства (используя теоремы 5.1 и 5.2), получим

, ,

откуда следует линейная зависимость системы . ■

Теорема 5.4 ( об однозначном задании линейного оператора ). Линейный оператор, действующий в конечномерном линейном пространстве, однозначно задается образами базисных векторов этого линейного пространства.

□ Пусть 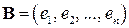– фиксированный базис в конечномерном линейном пространстве (). Выберем произвольную систему векторов . Покажем, что существует единственный линейный оператор 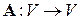, переводящий вектор в соответствующий вектор : .

Рассмотрим отображение 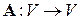, которое каждому вектору 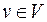, имеющему в базисе разложение

,

ставит в соответствие вектор по правилу

.

При всех : .

Покажем, что введенное отображение является аддитивным и однородным. Для любых векторов , и любого числа :

Существование линейного оператора доказано. Единственность доказывается методом от противного. ■