Структура линейного оператора

(образ, ядро, ранг, дефект, основные равенства)

Определение 5.3. Ядром 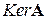линейного оператора 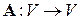называется множество векторов 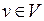таких, что :

.

Из определения видно, что ядром 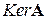линейного оператора 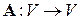являются те векторы пространства , которые переводятся оператором в нулевой вектор этого пространства.

Определение 5.4. Образом 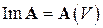линейного оператора 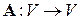называется множество всех векторов для каждого :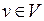

.

Теорема 5.5. Ядро 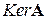и образ линейного оператора, действующего в линейном пространстве, являются подпространствами линейного пространства.

□ Для доказательства теоремы достаточно показать, что множества 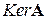и образ непустые и замкнуты относительно операций сложения векторов и умножения вектора на число.

Очевидно, что ядро 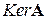является непустым, так как по теореме 5.1 образом нулевого вектора является нулевой вектор , то есть . Аналогично .

Покажем далее, что множество 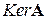замкнуто относительно операций сложения векторов и умножения вектора на число, то есть покажем, что если , то при всех 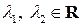: . Имеем

,

то есть .

Аналогично показывается, что множество замкнуто относительно операций сложения векторов и умножения вектора на число. ■

Поскольку по теореме 5.5 ядро и образ являются подпространствами линейного пространства, то можно говорить об их размерностях.

Определение 5.5. Дефектом линейного оператора называют размерность ядра 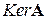этого оператора. Рангом линейного оператора называют размерность образа линейного оператора. Итак,

, .

Справедлива следующая теорема о дефекте и ранге линейного оператора.

Теорема 5.6 ( о размерностях ядра и образа линейного оператора ). Сумма дефекта и ранга линейного оператора, действующего в конечномерном линейном пространстве, равна размерности этого линейного пространства:

.

Доказательство. Пусть , . Выберем в подпространстве 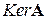базис и дополним его векторами до базиса 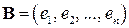всего пространства. Покажем, что векторы

образуют базис подпространства , то есть покажем, что эта система векторов линейно независима и любой вектор может быть представлен в виде линейной комбинации векторов . Если и , то

Равенство

означает, что вектор представлен в виде линейной комбинации векторов .

Покажем теперь, что система векторов линейно независима. Составим равенство

и покажем, что оно выполняется только в случае, когда .

Так как линейный оператор, то по теореме 5.2

.

Из последнего равенства следует, что вектор

.

Покажем, что

.

Отметим, что векторы порождают некоторое подпространство , являющееся линейной оболочкой этих векторов[1]: .

Покажем, что подпространства 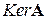и пересекаются только по нулевому вектору. Действительно, пусть . Тогда имеют место разложения вектора 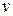по векторам базисов этих двух подпространств:

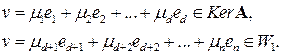
Вычитая из первого равенства второе, получим

.

Так как система векторов является базисом пространства (а значит, она линейно независима), то последнее равенство возможно только в том случае, когда . Это означает, что .

Выше было показано, что . Но . Значит, . Так как система векторов является линейно независимой, то последнее равенство возможно только в том случае, когда

.

Итак, система векторов образует базис подпространства , а значит, , что и доказывает справедливость утверждения теоремы. ■