 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейная модель международной торговли
|
|
Линейная модель международной торговли была предложена Д. Риккардо в XVIII веке. Будем предполагать, что 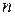 стран ведут торговлю. Обозначим через
стран ведут торговлю. Обозначим через 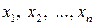 части национальных бюджетов этих стран, которые расходуются на покупку товаров. Эти величины называются национальными торговыми бюджетами.
части национальных бюджетов этих стран, которые расходуются на покупку товаров. Эти величины называются национальными торговыми бюджетами.
Пусть 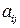 – доля бюджета
– доля бюджета 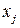 , которую
, которую 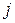 -я страна тратит на закупку товаров у
-я страна тратит на закупку товаров у 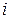 -ой страны. Введем матрицу коэффициентов
-ой страны. Введем матрицу коэффициентов 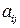
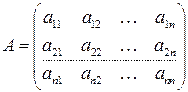 .
.
Так как национальный торговый бюджет расходуется только на закупки товаров внутри страны и вне ее, то справедливы равенства
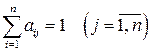 . (8)
. (8)
Определение. Матрицу 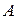 со свойством (8) называют структурной матрицей торговли.
со свойством (8) называют структурной матрицей торговли.
Равенства (8) означают, что для каждого столбца матрицы 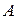 структурной торговли сумма элементов равна единице.
структурной торговли сумма элементов равна единице.
Можно показать, что условие сбалансированной (бездефицитной) торговли заключается в выполнении равенств
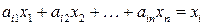 ,
, 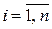 .
.
Введя в рассмотрение вектор-столбец национальных торговых бюджетов
 ,
,
условие сбалансированной (бездефицитной) торговли можно записать в матричной форме
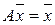 . (9)
. (9)
Уравнение (9) означает, что собственный вектор структурной матрицы торговли 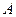 , соответствующий ее собственному значению
, соответствующий ее собственному значению 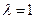 , состоит из национальных торговых бюджетов стран, удовлетворяющих условию бездефицитной международной торговли.
, состоит из национальных торговых бюджетов стран, удовлетворяющих условию бездефицитной международной торговли.
Пример 3. Задана матрица

структурной торговли. Требуется найти соотношение национальных доходов торгующих стран в сбалансированной системе международной торговли.
Решение. Представленная матрица является матрицей структурной торговли, так как выполняются равенства (8). Действительно,
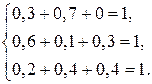
Найдем вектор-столбец национальных торговых бюджетов
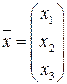 ,
,
пользуясь условием сбалансированной торговли (9), которое принимает вид
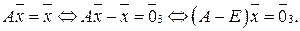
Так как матрица 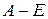 равна
равна
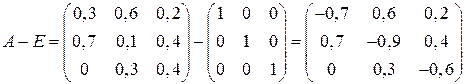 ,
,
то получаем однородную систему линейных алгебраических уравнений
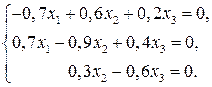
Перепишем ее в более удобном для решения виде (умножим обе части каждого уравнения на 10)
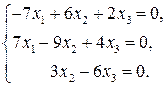
Решим последнюю систему методом Гаусса. Составляем расширенную матрицу этой системы и приводим ее к ступенчатому виду
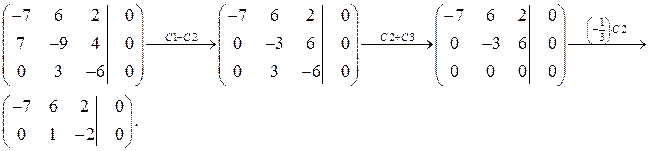
Переходя от последней ступенчатой матрицы к системе уравнений, получим
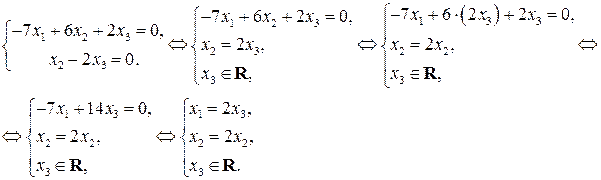
Итак, общее решение системы имеет вид
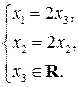
Это означает, что соотношение национальных доходов торгующих стран в сбалансированной системе международной торговли имеет вид 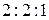 .
.
Дата публикования: 2015-07-22; Прочитано: 4002 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
