 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Критерии продуктивности модели
|
|
Математическую модель межотраслевого баланса (2) будем использовать для решения следующей задачи. Для периода времени  (например, год) известны вектор конечного потребления
(например, год) известны вектор конечного потребления  и матрица прямых затрат
и матрица прямых затрат 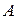 . Требуется определить вектор валового выпуска
. Требуется определить вектор валового выпуска  . Для этого необходимо решить систему линейных уравнений (2). В силу прикладного характера задачи все элементы матрицы
. Для этого необходимо решить систему линейных уравнений (2). В силу прикладного характера задачи все элементы матрицы 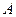 и векторов
и векторов  и
и  должны быть неотрицательными.
должны быть неотрицательными.
Определение 1. Матрицу 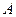 называют продуктивной, если для любого вектора
называют продуктивной, если для любого вектора  с неотрицательными элементами (
с неотрицательными элементами ( ) существует решение уравнения (2) – вектор
) существует решение уравнения (2) – вектор
 ,
,
все элементы которого неотрицательны ( ). В этом случае и модель Леонтьева называют продуктивной.
). В этом случае и модель Леонтьева называют продуктивной.
Определение 2. Матрицу
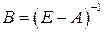 (3)
(3)
называют матрицей полных затрат. Элементы матрицы  называют коэффициентами полных затрат.
называют коэффициентами полных затрат.
Коэффициенты полных затрат показывают, какое количество продукции 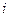 -й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечного продукта
-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечного продукта  -й отрасли.
-й отрасли.
Сформулируем далее критерии продуктивности матрицы прямых затрат.
Теорема 1. Матрица 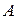 продуктивна тогда и только тогда, когда матрица полных затрат
продуктивна тогда и только тогда, когда матрица полных затрат
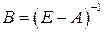
существует и все ее элементы неотрицательны (пишут  ). При этом вектор валового выпуска удовлетворяет условию
). При этом вектор валового выпуска удовлетворяет условию
 (4)
(4)
Теорема 2. Матрица 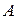 продуктивна, если максимум сумм ее элементов по каждому столбцу (каждой строке) не превосходит единицы:
продуктивна, если максимум сумм ее элементов по каждому столбцу (каждой строке) не превосходит единицы:
 , (5)
, (5)
причем хотя бы для одного столбца (любой строки)  .
.
Теорема 3. Матрица 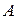 продуктивна тогда и только тогда, когда наибольшее собственное число матрицы
продуктивна тогда и только тогда, когда наибольшее собственное число матрицы 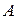 меньше единицы.
меньше единицы.
Пример 1. Заданы матрица
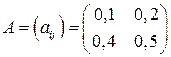
коэффициентов прямых затрат (технологическая матрица) и вектор

валового выпуска.
Требуется:
1) Составить статическую модель Леонтьева межотраслевого баланса, найти вектор  конечного потребления;
конечного потребления;
2) найти объем валового выпуска – вектор  , если вектор конечного потребления увеличить на вектор
, если вектор конечного потребления увеличить на вектор 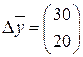 .
.
Дата публикования: 2015-07-22; Прочитано: 2280 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
