 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм нахождения запаса продуктивности модели Леонтьева
|
|
1. Составить матрицу 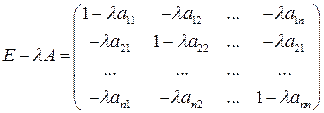 .
.
2. Вычислить определитель 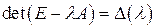 матрицы
матрицы 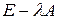 .
.
3. Составить матрицу 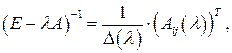 где
где 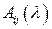 есть алгебраическое дополнение для элемента матрицы
есть алгебраическое дополнение для элемента матрицы 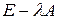 .
.
4. Решить систему неравенств
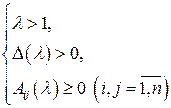 (6)
(6)
для определения искомого интервала 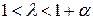 параметра
параметра 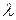 и запаса продуктивности
и запаса продуктивности 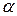 матрицы.
матрицы.
Пример 2. Найти запас продуктивности для матрицы
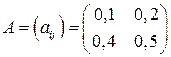
Решение. Заметим, что матрица является продуктивной, так как согласно теореме 2 максимум сумм ее элементов по каждому столбцу меньше единицы:
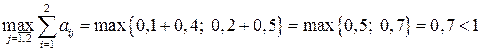 .
.
Аналогично можно показать, что максимум сумм ее элементов по каждой строке меньше единицы:
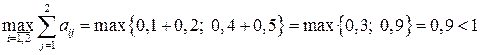 .
.
1) Составим матрицу
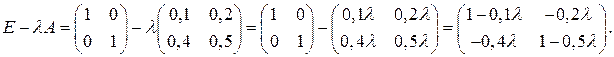
2) Вычислим определитель матрицы 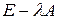
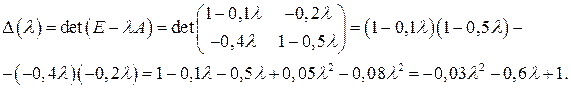
3) Составим матрицу
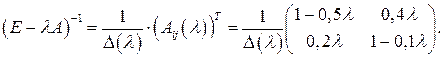
4) Для определения искомого интервала 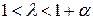 параметра
параметра 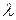 и запаса продуктивности
и запаса продуктивности 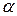 матрицы составим систему неравенств (6)
матрицы составим систему неравенств (6)
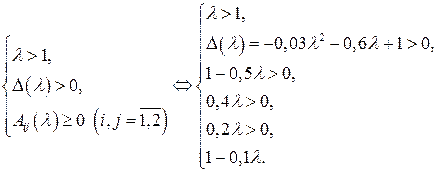
Полученную систему можно упростить, учитывая, что неравенства
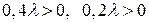
выполняются, так как 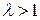 . Тогда необходимо решить систему
. Тогда необходимо решить систему
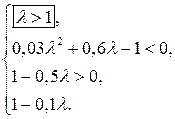 (7)
(7)
Квадратное неравенство
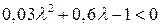
решаем через дискриминант
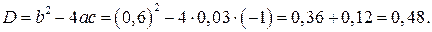
Находим корни квадратного трехчлена 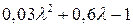 :
:
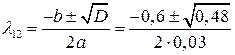 .
.
Имеем два корня (принимаем 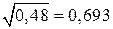 )
)
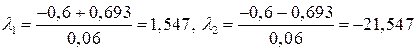 .
.
Тогда неравенство 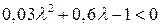 имеет решение – интервал
имеет решение – интервал
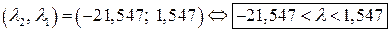 .
.
Линейные неравенства
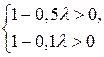
имеют соответственно решения
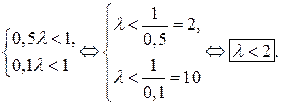
Итак, окончательно составим систему (7) из неравенств, заключенных в квадрат
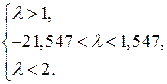
Решением последней системы неравенств является множество
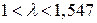 ,
,
откуда находим запаса продуктивности 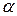 матрицы
матрицы
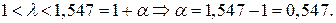
Ответ. Запас продуктивности модели Леонтьева 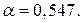
Дата публикования: 2015-07-22; Прочитано: 1829 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
