Построение касательной к окружности

Подобное построение основано на том, что касательная перпендикулярна к радиусу окружности, проведенному в точку касания.

Построение касательной к окружности в заданной на ней точке A (рисунок 43).Через точку A и центр окружности О проводят прямую и в точке А восстанавливают перпендикуляр к радиусу OA. Проведенный перпендикуляр MN и является искомой касательной.

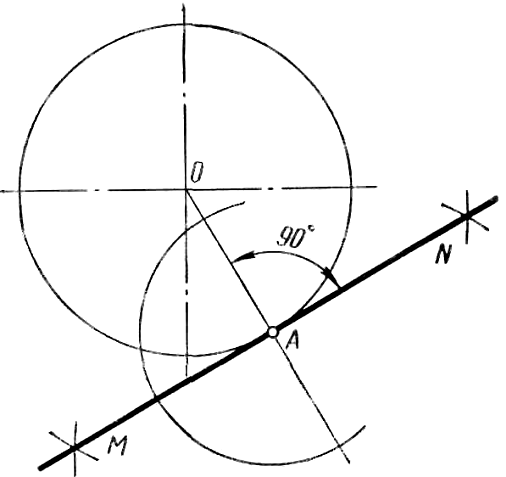
Рисунок 43

Построение касательной к окружности, если точка A задана вне окружности (рисунок 44). Центр окружности О и точку A соединяют прямой. Отрезок OA принимают за диаметр вспомогательной окружности. Разделив отрезок OA пополам, получают точку O₁ и из нее как из центра описывают вспомогательную окружность радиусом O₁A. Вспомогательная окружность пересекает заданную в точках B и C. Прямая, проведенная через точки А и B, будет касательной к окружности, так как угол АВО прямой как вписанный в окружность и опирающийся на ее диаметр. Прямая АС является второй касательной к заданной окружности.

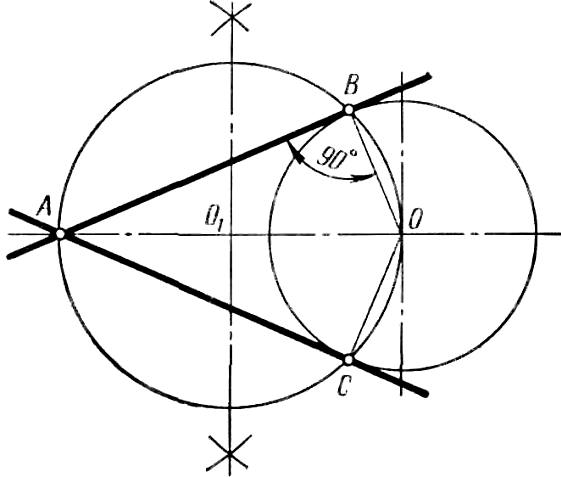
Рисунок 44