Справедлива и обратная теорема

Если точки A₁, B₁, C₁ расположены на сторонах AB, BC, CA треугольника ABC или на их продолжениях, так, что , то прямые AA₁, BB₁, CC₁ пересекаются в одной точке или параллельны.

Доказательство

Предположим, что прямые AA₁, BB₁ пересекутся в точке K, а прямая C C₁ не проходит через точку К.

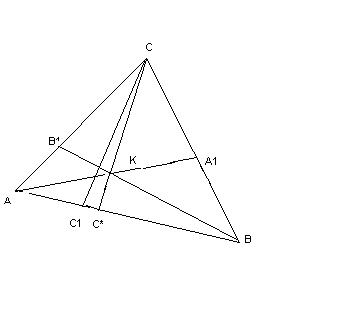
Соединим точку K с точкой C и продолжим полученную прямую до пересечения с прямой AB, получим точку С ¹. Тогда на основании прямой теоремы будем иметь:

, а по условию .

Следовательно, и точка С₁ совпадает с точкой C¹т.е. прямые AA₁, BB₁, CC₁ пересекаются в одной точке. Заметим, что если прямые AA₁ и BB₁ параллельны, то и прямая CC₁ им параллельна.

Прямая и обратная теоремы могут быть объединены в одну:

Пусть точки A₁, B₁, C₁ расположены на сторонах AB, BC, CA треугольника ABC или на их продолжениях. Для того, чтобы прямые AA₁, BB₁, CC₁ пересеклись в одной точке или были параллельны, необходимо и достаточно, чтобы .

8.8*.Теорема Менелая

Если треугольник ABC пересечен прямой, не параллельной стороне AB и пересекающей две его стороны AC и BC соответственно в точках B₁ и A₁ , а прямую AB- в точке C₁, то