 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема
|
|
Если прямые AA1, BB1, CC1, проходящие через вершины треугольника ABC, параллельны или проходят через одну точку, пересекают его стороны AB, BC, AC или их продолжения в точках A1, B1, C1, соответственно, то справедливо равенство
Доказательство.
Рассмотрим первый случай: прямые пересекаются в одной точке K.
Проведем чрез вершину A прямую NM, параллельно BC.Из подобия треугольников AMC1 и BCC1 будем иметь:
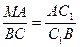(1).
Из подобия треугольников ANC1 и CBB1 будем иметь: 
(2).
Далее: 
, 
(3).
Перемножим равенства (1), (2), (3), получим
Рассмотрим второй случай, когда прямые AA1, BB1, CC1 параллельны.
Тогда 
(4), 
(5), 
(6), перемножив равенства (4),(5),(6), получим . Теорема доказана.
Дата публикования: 2015-07-22; Прочитано: 362 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
