Периметр треугольника, отсекаемого от данного касательной к

вписанной в треугольник окружности, равен удвоенному отрезку стороны от вершины треугольника до точки касания,

P_AMN = 2AK.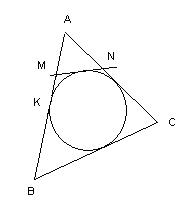

9. 3*. Сумма обратных величин высот треугольника равна обратной величине радиуса вписанного круга:

9. 4**.Площадь треугольника, вершинами которого служат точки касания вписанного круга, равна .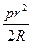

9.5**.Расстояние от центра вписанной в треугольник окружности доточки пересечения медиан треугольника равно

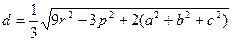
9.6**.Расстояние от центра описанной окружности до ортоцентра равно

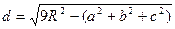
9.7.**Расстояниемежду центрами вписанной и описанной окружности равно d =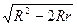

9.8**.Во всяком треугольнике сумма расстояний от центра описанного круга до сторон треугольника равна сумме радиусов вписанного и описанного кругов (теорема Карно).

10. 6*.Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей.

10.9.* Угол между высотами параллелограмма равен острому углу параллелограмма.

11.7*. Середины сторон ромба являются вершинами прямоугольника.

12.3**. Суммы квадратов расстояний от некоторой точки плоскости прямоугольника до двух его противоположных вершин равны.

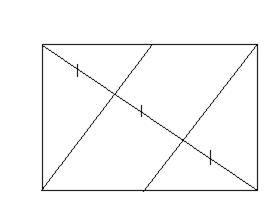
12.5*.Отрезки от вершины прямоугольника до середины противолежащей стороны делят пересекающую их во внутренних точках диагональ прямоугольника на три равные части.