Денежный рынок и кривая LM

Кривая LM – это кривая равновесия на денежном рынке. Она фиксирует все комбинации Y и r, которые удовлетворяют функции спроса на деньги при заданной Центральным Банком величине денежного предложения MS. Во всех точках кривой LM спрос на деньги равен их предложению. Сам термин LM отражает это равенство (Liquidity Preference = Money Supply) (см. рис.8.3).

Рисунок 8.3 - Графический вывод кривой LM с помощью равновесия на денежном рынке

Рис. 8.3(а) показывает денежный рынок: рост дохода от Y₁ до Y₂, увеличивает спрос на деньги и, следовательно, повышает ставку процента от R_l до R₂.

Рис. 8.3(б) показывает кривую LM: чем выше уровень дохода, тем выше ставка процента.

Уравнение кривой LM может быть получено путем решения 5-го уравнения модели IS-LM (функция спроса на деньги) относительно r и Y. Из этого уравнения получаем значение уровня равновесного дохода:

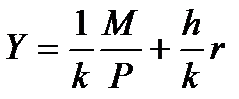
и значение равновесной ставки процента:

Сдвиги кривой LM обусловлены изменением номинального предложения денег (М^S). Поскольку уровень цен фиксирован (Р=соnst), то изменение центральным банком количества денег в обращении, меняет реальное предложение денег (М/Р)^S. Так как коэффициент при (М/Р)^S в уравнении 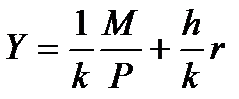положительный, то рост предложения денег ведет к сдвигу кривой вправо на расстояние ΔМ(1/k), в то время как его сокращение сдвигает кривую на такое же расстояние влево.

Наклон кривой LM. Наклон кривой LM равен коэффициенту(k/h), он определяет сравнительную эффективность фискальной и монетарной политики и зависит от двух параметров:

1) чувствительности спроса на деньги к уровню дохода (k);

2) чувствительности спроса на деньги к ставке процента (h).
Уменьшение h увеличивает наклон кривой LM (она становится более крутой) и при h = 0 кривая становится вертикальной. При росте h кривая LM становится более пологой. При уменьшении k кривая LM будет более пологой, а при его увеличении – более крутой.