Форми рядів розподілу та їх характеристика

Різноманітність статистичних сукупностей – передумова різних форм співвідношення частот і значень ознаки, що варіює. За своєю формою ряди розподілу поділяють на такі види: одно-, дво- і багатовершинні. Наявність двох і більше вершин свідчить про неоднорідність сукупності, про поєднання в ній груп з різними рівнями ознаки. Ряди розподілу якісно однорідних сукупностей, як правило, одновершинні. Серед одновершинних рядів розподілу є симетричні (скошені), гостро- і плосковершинні.

У симетричному розподілі рівновіддалені від центру значення ознаки мають однакові частоти, в асиметричному – вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена вліво, то це правостороння асиметрія і, навпаки. Асиметрія виникає внаслідок обмеженої варіації в одному напряму або під впливом домінуючої причини розвитку, яка веде до зміщення центру розподілу.

Найпростішою мірою асиметрії є відхилення між середньою арифметичною і медіаною або модою.

В симетричному розподілі характеристики центру мають однакові значення М_е=М_о.

В асиметричному між ними існують певні розбіжності. За правосторонньої асиметрії > М_е> М_о,за лівосторонньої асиметрії, навпаки, < М_е< < М_о.

Стандартизовані відхилення або 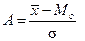характеризують напрям і ступінь скошеності розподілу. В симетричному розподілі А = 0, за правосторонньої асиметрії А > 0; за лівосторонньої А < 0.

– лівостороння (асиметрія) – правостороння (асиметрія)

– гостровершинний (ексцес) – плосковершинний (ексцес)

Рис. 6.1. Різновиди форм розподілу

Приклад. Маємо такі дані про розподіл працівників за заробітною платою.

Таблиця 6.7 – Визначення форми розподілу працівників за заробітною

платою

Групи працівників за заробітною платою, грн. (хі)	Частка працівників у загальній чисельності, % (wi)
50—100				-159	25 281	126 405
100—150			1 625	-109	11 881	154 453
150—200-			5 600	-59	3 481	111 392
200—250			5 625	-9		2 025
250—300			6 875		1 681	25 215
300—350			3 250		8 281	82 810
Разом	100,0	–	23 350	–	–	502 330

грн.;

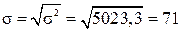грн.;

грн.;

.

Стандартизоване відхилення свідчить про незначну правосторонню асиметрію, а тому розподіл можна вважати симетричним.

Гостровершинність розподілу відображає скупченість значень ознаки навколо середньої величини і називається ексцесом. На практиці часто в одному розподілі поєднуються всі названі особливості: одновершинний розподіл може бути симетричним і гостро вершинним, або скошеним і плосковершинним.

Як узагальнюючі характеристики розподілу використовують моменти. За допомогою невеликого їх числа можна описати будь-який розподіл. Момент розподілу – це середня арифметична k -го ступеня відхилень х – А.

Залежно від величини А моменти поділяють на первинні А = 0, центральні А= й умовні А = const. Ступінь k визначає порядок моменту. На практиці використовуються:

Початкові моменти:

– нульового порядку (k = 0)

– першого порядку (k = 1)

– другого порядку (k = 2)

– третього порядку (k = 3)

– четвертого порядку (k = 4)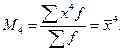

Початкові моменти відносно х ₀(умовні):

– нульового порядку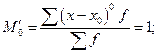

– першого порядку

– другого порядку

– третього порядку

– четвертого порядку

Центральні моменти:

– нульового порядку

– першого порядку

– другого порядку

– третього порядку

– четвертого порядку

Первинний момент першого порядку – це середня арифметична , другого – середній квадрат значень ознаки Центральний момент другого порядку характеризує варіацію третього – асиметрію, четвертого – ексцес.

Для порівняння ступеня асиметрії різних розподілів, використовують стандартизований момент:

Вважають, що при А < 0,25 асиметрія низька, якщо А не перевищує 0,5 – середня і при А > 0,5 – висока.

Для вимірювання ексцесу використовують аналогічно побудований коефіцієнт, тобто стандартизований момент четвертого порядку:

У симетричному розподілі Е = 3, при гостро вершинному – Е > 3, плоско вершинному Е < 3.

Оцінка нерівномірності розподілу значень ознаки між окремими складовими сукупностей ґрунтується на порівнянні часток двох розподілів – за кількістю елементів сукупності d_j та за обсягом значень ознаки D_j. Якщо розподіл значень ознаки рівномірний, то d_j = D_j. Відхилення часток свідчить про певну нерівномірність розподілу, яка вимірюється коефіцієнтами: концентрації та локалізації.

Коефіцієнт концентрації (К)є узагальнюючою характеристикою відхилення розподілу від рівномірного.

Коефіцієнт концентрації – це напівсума модулів відхилень:

Межа коливання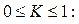

– при рівномірний розподіл;

– при повна концентрація;

– чим більший ступінь концентрації, тим більше значення К.

Коефіцієнти концентрації використовуються в регіональному аналізі для оцінювання рівномірності територіального розподілу виробничих потужностей, фінансових ресурсів тощо.

Коефіцієнт локалізації (L_j) розраховується для кожної j -ї складової сукупності.

За рівномірного розподілу всі значення L_j= 1. У випадку концентрації значень ознаки в j -й складовій L_j >1 і, навпаки.

Розрахунок коефіцієнтів К та L_j показано у табл. 6.8 на прикладі розподілу підприємств за вартістю реалізованої продукції.

Таблиця 6.8 – Розрахунок коефіцієнтів концентрації та локалізації

Вартість реалізованої продукції, тис.гр.од.	% до підсумку
кількість підприємств, dj	вартість реалізованої продукції, Dj.
До 2		2	0,17
2 – 5			0,28
5 – 10			0,52
10 – 20			1,12
20 – 40			2,87
40 і більше			8,00
Разом:			×

Коефіцієнт концентрації становить

або 0,45,

що свідчить про відносно високий рівень концентрації у підприємствах. Обсяги товарної продукції концентруються у великих підприємствах – в останній групі L_j = 8,00.

Коефіцієнти концентрації та локалізації є ефективним засобом вимірювання диференціації сукупності за даними інтервальних рядів з нерівними інтервалами та за даними атрибутивних рядів. За аналогією з коефіцієнтом концентрації розраховують коефіцієнт подібності(схожості) структур двох об'єктів або одного об'єкта за двома ознаками:

Якщо структури однакові, то Р = 1. Чим більші відхилення структур, тим менше значення коефіцієнта Р.

Для оцінки інтенсивності структурних зрушеньу часі використовують абсолютні ступені варіації – середнє лінійне або середнє квадратичне відхилення часток, які називають коефіцієнтами структурних зрушень:

лінійний;

квадратичний,

де та – частки розподілу за два періоди;

т – число складових сукупності.

Розрахунок лінійного коефіцієнта структурних зрушень доходів від телекомунікаційних послуг зв’язку наведено в табл. 6.9.

Таблиця 6.9 – Структура доходів від надання телекомунікаційних послуг

Вид зв’язку	% до підсумку	Структурні зрушення, відсоткові пункти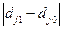
2007 р.	2008 р.
Мобільний зв'язок	64,86	68,30	3,44	3,44
Телефонний фіксований зв’язок	25,06	21,91	–3,15	3,15
Широкосмуговий доступ	4,13	5,59	1,46	1,46
Передавання й приймання телевізійних та радіопрограм	2,84	3,26	0,42	0,42
Супутниковий зв’язок	0,18	0,23	0,05	0,05
Проводове мовлення	0,26	0,47	0,21	0,21
Телеграфний зв’язок	0,16	0,12	– 0,04	0,04
Всього:	100,00	100,00	0,00	8,77

За даними таблиці в.п., тобто структура доходів від телекомунікаційних послуг змінилася в середньому на 1,25 відсоткових пункти.