Преобразования Лоренца

Анализ явлений в инерциальных системах отсчета, проведенный А. Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними и, следова­тельно, должны быть заменены преобразо­ваниями, удовлетворяющими постулатам теории относительности.

Эти преобразования предложены Лоренцом в 1904 г., еще до появления теории относительности, как преобразования, относительно которых уравнения Макс­велла инвариантны.

Рассмотрим две инерциальные системы отсчета: К (с координатами x,y, z) и К' (с координатами x′, y′, z′), движущуюся относительно К вдоль оси x со скоростью = const (рис.5.2).

Преобразования Лоренца в этом случае имеют вид

К К' К′′ К

x′ = , x = ,

y′ = y, y = y′, (5.5)

z′ = z, z = z′,

t′ = , t = ,

β = υ / c.

Из сравнения приведенных уравнений вытекает, что они симметричны и отличаются лишь знаком при 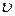. Это очевидно, так как если скорость движения системы К' относительно системы К равна 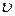, то скорость движения К относительно К' равна (- ).

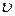Из преобразований Лоренца вытекает также, что при малых скоростях (по сравнению со скоростью света), они переходят в классические преобразования Галилея.

Из преобразований Лоренца следует очень важный вывод о том, что как рассто­яние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках пре­образований Галилея эти величины счита­лись абсолютными, не изменяющимися при переходе от системы к системе. Таким образом, теория Эйнштейна оперирует не с трехмерным простран­ством, к которому присоединяется понятие времени, а рассматривает неразрывно свя­занные пространственные и временные ко­ординаты, образующие четырехмерное пространство-время.