Йкеліс бұрышы және үйкеліс конусы

Жоғарыда айтылған үйкеліс заңдарын көрнекі түрде түсіндіру үшін үйкеліс бұрышы мен үйкеліс конусы ұғымдарын енгізген ыңғайлы.

Актив күштер әсеріндегі дене тепе-теңдіктің шектік жағдайында болсын делік. Бұл жағдайда үйкеліс күші 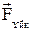өзінің максимал мәніне 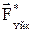жетеді, реакция күші де өзінің максимал мәніне өседі. Ол үйкелісетін денелердің жанасу беттеріне ортақ нормальмен максимал бұрыш құрады.

Сонымен, үйкеліс бұрышы деп максимал толық реакция мен жанасушы беттерге түсірілген ортақ нормаль арасындағы ең үлкен j₀ бұрышты айтады (1.26 сурет). 1.26 сурет бойынша:

.

Бірақ , сондықтан үйкеліс бұрышы мен үйкеліс коэффициенті арасындағы мына байланысты аламыз:

. (1.6.4)

максимал толық реакция векторының геометриялық орны төбесі денелердің жанасу нүктесінде жататын конустық бетті береді. Бұл конус үйкеліс конусы деп аталады. Егер сырғанау үйкеліс коэффициенті қозғалыстың барлық бағытында бірдей болса, бұл конус дөңгелек конус болады (1.26 сурет). Егер үйкеліс коэффициенті мүмкін қозғалыс бағытына тәуелді болса, үйкеліс конусы дөңгелек болмайды.

Енді үйкеліс конусын пайдаланып кедір-бұдырлы жазықтықта жатқан дененің тепе-теңдік шартын алайық. Денеге әсер ететін барлық актив күштерді нормальмен бұрыш құратын 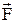күшпен алмастырамыз (1.27 сурет). Тепе-теңдік шарттарын құрамыз:

Осы теңдеулерден мынаны аламыз:

.

Тепе-теңдік кезінде (1.6.3) шарты орындалатынын ескерсек 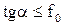немесе , демек тепе-теңдік кезінде болатынын аламыз. Бұл шарт әсер етуші 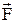күшінің сан шамасына тәуелді емес. Олай болса, кедір-бұдырлы жазықтықта жатқан дене тепе-теңдікте болу үшін денеге әсер ететін актив күштердің тең әсерлі күшінің әсер ету сызығы үйкеліс конусының ішімен немесе оның құраушысымен бағытталуы қажет және жеткілікті. Бұлай болмаған жағдайда, яғни 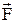күшінің әсер ету сызығы үйкеліс конусының сыртымен өтсе, дене тепе-теңдікте болмайды. Нормальмен бұрыш құратын ешқандай күшпен денені жазықтық бойымен қозғалтуға болмайды. Денелердің қысылып қалуын немесе өзінен өзі тоқтап қалуын осымен түсіндіруге болады.