Кинематические уравнения вращательного движения

Так же, как в случае поступательного движения, пользуясь определением угловой скорости (2.31), найдём выражение, задающее угол поворота в функции времени:

d j = w dt; Þ .

(2.43)

Для случая равномерного вращения постоянная величина w выносится за знак интеграла и угол поворота будет линейной функцией времени:

j = j0 + w t,

(2.44)

где j ₀ – угол, определяющий положение тела в начальный момент времени.Полученное уравнение нетрудно несколько изменить, введя N – число полных оборотов, сделанных вращающимся телом за время t. Поскольку один оборот соответствует углу в 2 p радиан, то

j =2p N.

(2.45)

Характеризуя вращение, очень часто пользуются частотой вращения n = dN/dt. Эта величина задаёт число оборотов в единицу времени. Учитывая вновь, что один оборот составляет 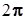радиан, получим, что:

w =2pn.

(2.46)

Единица измерения частоты вращения об/с, а размерность – с^–1.

Используя две вновь введенные величины и полагая начальный угол равным нулю, можно представить уравнение (2.44) в виде:

N = n t.

(2.47)

Заметим, что последнее равенство, так же как и исходное (2.44), справедливо лишь для равномерного вращения, и его нельзя использовать в случае, если есть ускорение – вращение замедляется либо ускоряется. В этих случаях интегрирование в (2.43) невозможно до тех пор, пока не найдена зависимость угловой скорости от времени. Определение углового ускорения (2.35) дает возможность найти эту зависимость:

d w = e dt,

(2.48)

и, полагая, что в момент времени t = 0 угловая скорость равна w ₀ и угловое ускорение постоянно, получим:

; Þ w = w0 ± e t.

(2.49)

Знак минус в последнем равенстве имеет место для случая отрицательного ускорения, то есть для случая равнозамедленного вращения.

Подставляя последнюю формулу в интеграл (2.43), получим уравнение для определения угла поворота, как функции времени (при j ₀ = 0):

.

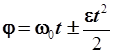(2.55)

Вновь, как и при поступательном движении, имеем два уравнения (для угла поворота и угловой скорости) для равнопеременного вращения.

В случае не равнопеременного вращения (e ¹ const) угловая скорость и угол поворота могут быть также найдены интегрированием, если известна зависимость e (t).

Обратная задача – нахождение угловых скорости и ускорения по заданной зависимости угла поворота от времени j (t) – решается, как и в случае кинематики точки, дифференцированием:

w = j¢;e = w¢ = j¢¢.

(2.56)

Уравнения кинематики вращательного движения получены нами лишь аналитическим путем – интегрированием уравнений, вводящих понятие угловой скорости как производной от угла поворота и понятие углового ускорения как производной от угловой скорости. Графический метод здесь опущен. Полученные уравнения аналогичны уравнениям кинематики точки. Ниже приведена табл. 2.1, отражающая эту аналогию.

Таблица 2.1

Понятия кинематики	Поступательное движение	Вращательное движение
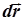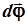Перемещение Путь Скорость Ускорение	s u a t	j w e
Частные случаи
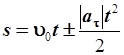
Равномерное Уравнение пути Равнопеременное Уравнение скорости Уравнение пути	u = const s = u t a = const u = u0 ± | a t| t	w = const j = w t; N = n t e = const w = w0 ± e t
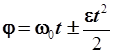
Общий случай
Задано Скорость Ускорение	s (t) u = s ¢ a t= u¢ = s ¢¢	j(t) w = j¢e = w¢ = j¢¢

В таблице опущены частные случаи уравнений равнопеременного движения (как поступательного, так и вращательного), которые сводятся к одночленным уравнениям пути и скорости.