И их связь с линейными характеристиками

Вращение отличается от поступательного движения тем, что точки тела в этом случае описывают концентрические окружности разных радиусов, то есть движутся не одинаково. Кроме того, имеется совокупность неподвижных точек, называемых осью вращения.

Очевидно, что путь, пройденный каждой точкой за одно и то же время будет разным, различной будет и скорость движения. Не составляет труда найти такую величину, которая описывала бы перемещение тела и оставалась бы одинаковой для всех его точек. Такой величиной будет бесконечно малый угол поворота d j. Из геометрии известно, что он связан с дугой ds окружности через ее радиус:

ds = Rd j.

(2.28)

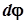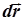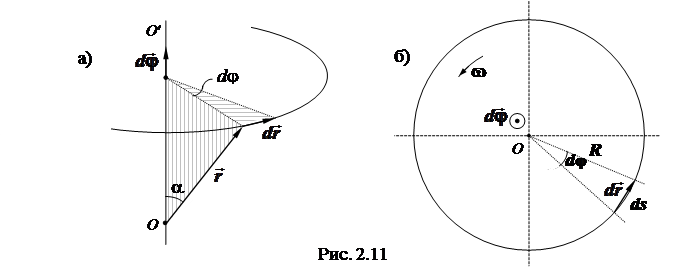
Для характеристики направления вращения принято считать величину вектором, направление которого следует увязать с заданными уже векторами и , которые перпендикулярны друг другу (рис. 2.11).

Если направить вектор по оси вращения, связав его направление с направлением вращения правилом буравчика, то вектор перемещения 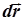будет равен векторному произведению векторов и :

,

(2.29)

то есть вектор перемещения направлен перпендикулярно плоскости, в которой лежат вектора и (вертикальная штриховка на рис. 2.11а). Изменение порядка написания векторов и , очевидно, изменит знак векторного произведения на противоположный.

Из рис. 2.11 следует, что модуль вектора перемещения

, или ,

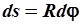(2.30)

что совпадает с выражением (2.28). На рис.2.11(б) представлен вид сверху на рис. 2.11(а), вдоль оси О'О. Вектор 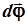на этом рисунке направлен "к нам", что показано кружком с точкой посередине.

Введём вектор угловой скорости, который будет характеризовать как быстроту, так и направление вращения:

.

(2.31)

Направление совпадает с 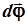, то есть с осью вращения и определяется по правилу буравчика. Дифференцируя (2.29) по времени, получим связь между угловой скоростью и линейной скоростью точки:

,

(2.32)

или

.

(2.33)

Раскрывая векторное произведение, получим выражение для модуля линейной скорости:

,

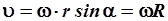(2.34)

так как r sina = R (см. рис. 2.11).

Определим теперь угловое ускорение как быстроту изменения угловой скорости во времени:

.

(2.35)

Вектор , так же, как и векторы угловой скорости и углового перемещения, направлен по оси вращения. При ускоренном вращении (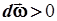) его направление совпадает с вектором угловой скорости, при замедленном вращении (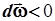) вектор углового ускорения направлен противоположно вектору . Если направление оси вращения изменяется, то вектор не совпадает с осью вращения, но всегда остается направленным по вектору .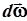

Связь углового ускорения с линейным ускорением получим, дифференцируя (2.33) по времени:

(2.36)

или:

.

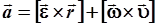(2.37)

Таким образом, линейное ускорение вращающейся точки рано сумме тангенциального

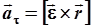
(2.38)

и нормального

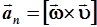
(2.39)

ускорений: .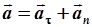

Раскрывая векторное произведение (2.38), получим:

a t=e rsin a= e R,

(2.40)

то есть тангенциальное ускорение точки пропорционально радиусу окружности, по которой эта точка движется. Отметим, что при замедленном вращении ускорения e и a _t отрицательны.

Величину нормального ускорения найдем, раскрывая векторное произведение (2.39):

.

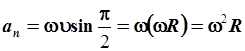(2.41)

Модуль полного ускорения вращающейся точки

.

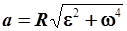(2.42)

Уместно обсудить вопрос о размерностях (единицах измерения) введённых выше кинематических характеристик вращения. Их три: угол поворота, угловая скорость и угловое ускорение. Угол поворота измеряется в радианах (рад), а не в градусах. Радиан – безразмерная величина, т.к. определяется по отношению длины дуги к радиусу, следовательно, угол поворота или угловое перемещение – величина безразмерная. Угловая скорость, следовательно, измеряется в рад/с, а ускорение – в рад/с². Соответствующие размерности: [ w ] = c^–1; [ e ] = c^–2.