Алгоритм Литтла

Пусть известна матрица весов некоторого орграфа, вершины которого занумеруем числами от 1 до :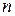

,

где 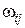– вес дуги, соединяющей вершины 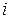и ,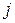

Символ 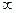ставится для блокировки дуг графа, которые явно не включаются в гамильтонов цикл, т.е. в расчет не берутся дуги и . Можно показать, что оптимальность решения не изменяется при прибавления некоторого числа к строке или столбцу матрицы .

Алгоритм Литтла разбивается на несколько шагов.

Шаг 1. Приведение исходной матрицы.

В каждом столбце и в каждой строке матрицы нужно получить хотя бы один нуль. Для этого, например, в первом столбце выберем минимальный элемент и вычтем его из всех элементов первого столбца. Аналогично поступим с остальными столбцами. Если при этом в некоторых строках не появляются нули, то для них осуществим ту же процедуру.

После этого вычислим константу приведения – сумму минимальных элементов столбцов и строк, использованных для преобразования матрицы . Получим приведенную матрицу с константой приведения .

Шаг 2. Определение степеней нулей.

Найдем степени каждого нуля – сумму минимальных элементов строки и столбца , в которых стоит этот нуль, без учета самого нуля. Нуль с максимальной степенью определяет дугу , которая вероятнее всего войдет в гамильтонов цикл. Например, если нуль с максимальной степенью находится на пересечении второй строки и третьего столбца, то дуга , вероятнее всего, войдет в гамильтонов цикл.

Шаг 3. Ветвление.

На самом деле, дуга, соответствующая максимальной степени нуля, может, как входить в гамильтонов цикл, так и не входить в него. Поэтому следует рассмотреть сразу два случая.

Первый случай. Возможно, дуга вошла в гамильтонов цикл. Блокируем ее, полагая . Строку 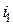и столбец вычеркиваем. Если требуется, приводим полученную матрицу меньшего порядка с константой приведения .

Второй случай. Дуга не вошла в гамильтонов цикл. Полагаем . Если требуется, приводим полученную матрицу с константой приведения .

Если , то шаги 2, 3 повторяем с матрицей .

Если , то шаги 2, 3 повторяем с матрицей . И так до тех пор, пока не дойдем до матрицы второго порядка, содержащей два нуля:

,

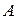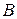где и – некоторые числа или . Нули соответствуют двум последним дугам гамильтонова цикла: , при этом .

Если , где 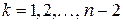, то задача решена. Если же для некоторого получается , то всю процедуру следует провести с матрицей . На последнем этапе получим новое значение функции . Это значение сравниваем с , то есть процесс продолжается до тех пор, пока новые значения не станут меньше .

С помощью метода ветвей и границ с использование современного программного обеспечения ЭВМ можно решать задачи коммивояжера для 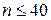. В связи с малой эффективностью точных методов получили широкое применение эвристические. В настоящее время существует более ста приближенных методов решения задачи коммивояжера, среди которых наиболее прост метод ближайшего соседа. Он реализует требование включения в искомый замкнутый цикл вершины, ближайшей к только что найденной. Алгоритм метода состоит в последовательном добавлении к начальной вершине следующей ближайшей к ней и т.д. Метод очень прост, однако степень приближения к оптимальному решению существенно зависит от выбора начальной вершины. Поэтому алгоритм целесообразно применить к каждой из вершин, как к начальной, и только затем выбрать замкнутый цикл наименьшей длины. Отметим, что если ближайший сосед для некоторой вершины уже вошел в цикл, то берется следующая по близости вершина и т.д. Например, используя данный метод для полного взвешенного графа с 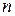вершинами, потребуется рассмотреть гамильтоновых циклов, из которых выбирается цикл наименьшей длины.

Классическая задача коммивояжера, только в несколько иной формулировке, нашла применение и при организации производства в машиностроении – задача о переналадке оборудования при переходе линии на обработку деталей, схожих по конструкции и габаритам.

Пример 4.2. На одной и той же поточной линии предприятие может обрабатывать пять видов деталей. Время наладки при переходе линии на обработку от одного вида деталей к другому представлена матрицей , где − затраты времени (часы) на наладку переменно-поточной линии при переходе к обработке деталей от 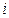-го вида к деталям -го вида. С помощью алгоритма Литтла найти последовательность перестройки линии с одной детали на другую, при которой должны быть обеспечены минимальные общие потери рабочего времени на ее переналадки.

.

Решение. Сначала получим приведенный вид данной матрицы. В каждом столбце определим минимальный элемент и запишем его в нижней строке:

.

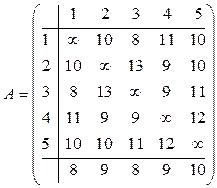Из каждого элемента столбца вычтем соответствующий минимальный элемент и получим матрицу :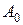

.

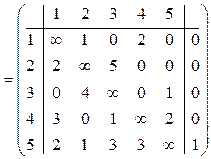Матрица 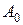не является приведенной, поэтому определим минимальный элемент в каждой строке и вычтем его из всех элементов соответствующей строки. В результате получим приведенную матрицу :

.

Вычислим константу приведения :

.

Найдем степени каждого нуля – сумму минимальных элементов строки и столбца, в которых стоит нуль. К каждому нулю припишем вверху его степень:

.

Максимальная степень равна 1. Нули с максимальной степенью определяют дуги, которые вероятнее всего войдут в гамильтонов цикл. В нашем случае наиболее вероятными дугами гамильтонова цикла являются .

Выберем дугу . В связи с этим рассмотрим две матрицы: и . В матрице уберем первую строку и третий столбец, элемент заменим на . В матрице элемент заменим на . Получим:

, .

Обе матрицы не являются приведенными. Для их приведения определим минимальные элементы столбцов и выполним их вычитание из элементов соответствующих столбцов:

, .

В результате получим следующие приведенные матрицы и .

, .

Вычислим константы приведения:

, ,

где и – суммы минимальных элементов строк и столбцов матриц и .

Так как , то далее будем рассматривать матрицу , поскольку ее размерность меньше, чем размерность матрицы . Определим степени нулей матрицы :

.

Максимальная степень – число 2. Наиболее вероятной дугой гамильтонова цикла является дуга .

В связи с этим рассмотрим две матрицы: и . В матрице уберем строку под номером четыре и столбец под номером два, элемент заменим на . В матрице элемент заменим на . Получим:

, .

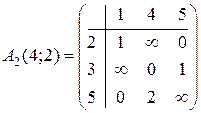Матрица получена приведенной. Матрица не является приведенной. Определим минимальные элементы строк матрицы и вычтем их из элементов соответствующих строк:

.

Вычислим константы приведения:

,

.

Так как , то далее будем рассматривать матрицу , для которой определим степени каждого нуля:

.

Максимальная степень – число 3. Наиболее вероятными дугами гамильтонова цикла являются дуги и .

Выберем дугу . В связи с этим рассмотрим две матрицы: и . В матрице уберем строку под номером три и столбец под номером четыре. В матрице элемент заменим на . Получим:

, .

Матрица - приведенная. Матрица не является приведенной. Определим минимальные элементы строк и столбцов матрицы и выполним приведение:

.

Вычислим константы приведения:

,

.

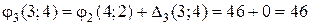Так как , то рассмотрим матрицу . Последние две дуги гамильтонова цикла определим из этой матрицы: и .

Сравним константу приведения с константами приведения альтернативных вариантов ():

: ;

: ;

: .

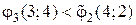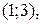
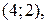
Так как (), то полученное решение, состоящее из дуг , является оптимальным, но не единственным.

Весь процесс поиска оптимального плана можно изобразить в виде дерева ветвления, рис. 4.4.

Рис. 4.4

Из полученных дуг составим замкнутый гамильтонов цикл: , который можно представить в виде орграфа:

Построенный гамильтонов цикл соответствует последовательности перестройки линии с обработки одной детали на другую, что означает следующее: после обработки деталей первого вида следует наладить обработку деталей третьего вида: после третьего – четвертого вида; после четвертого – второго вида; после второго – пятого вида; после пятого – снова вернуться к обработке первого вида деталей. При этом минимальные общие потери рабочего времени составят часов.

Ответ:

последовательность перестройки линии: ;

минимальные общие потери рабочего времени составят 46 часов.,

5. СЕТИ. ПОТОКИ В СЕТЯХ

5.1.Сеть. Поток в сети

Функциональное назначение большинства физически реализованных сетей состоит в том, что они служат носителями систем потоков, т.е. систем, в которых некоторые объекты текут, движутся или транспонируются по системе каналов (дуг сети) ограниченной пропускной способности. Приведем некоторые примеры практических задач.

1. Пусть имеется сеть автомобильных дорог, по которым можно проехать из пункта 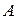в пункт 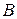. Дороги могут пересекаться в промежуточных пунктах. Количество автомобилей, которые могут проехать по каждому отрезку дороги в единицу времени, не безгранично, оно определяется такими факторами, как ширина проезжей части, качество дорожного покрытия, действующие ограничения скорости движения и т.д. (обычно данную характеристику называют «пропускной способностью» дороги). Каково максимальное количество автомобилей, которые могут проехать из пункта 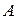в пункт 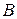без образования пробок на дорогах (эту величину называют «автомобильным потоком»)? Можно также поставить другой вопрос: какие дороги и насколько можно расширить или улучшить, чтобы увеличить максимальный поток на заданную величину?

2. Пусть имеется сеть трубопроводов, соединяющих пункт 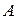(например, нефтепромысел) с пунктом 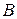(нефтеперерабатывающим заводом). Трубопроводы могут соединяться и разветвляться в промежуточных пунктах. Количество нефти, которое может быть перекачано по каждому отрезку трубопровода в единицу времени, также не безгранично и определяется такими факторами, как диаметр трубы, мощность нагнетающего насоса и т.д. (данная характеристика называется «пропускной способностью» или «максимальным расходом» трубопровода). Сколько нефти можно пропускать через такую сеть в единицу времени?

Изучение данных практических задач и многочисленных им подобных приводит к теории потоков в сетях. Данная теория разрабатывает решения общей задачи, которая называется задача об оптимальном потоке. Рассмотрим частный случай этой задачи, а именно, задачу определения максимальной величины потока.

Определение 5.1. Сетью называется связный ориентированный граф 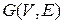без петель с выделенными вершинами 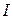- истоком и 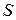- стоком, причем каждой дуге поставлено в соответствие некоторое натуральное число – пропускная способность дуги.

Напомним, что истоком называется вершина, у которой , т.е. из которой дуги только выходят; а стоком – вершина, у которой , т.е. вершина, в которую дуги только входят.

Пропускная способность дуги характеризует максимальное количество вещества, которое может пропустить за единицу времени дуга 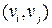. На сети пропускную способность дуги будем записывать в круглых скобках.

Поток в сети определяет способ пересылки некоторых объектов из одной вершины графа в другую по направлению дуги. Число объектов (количество вещества) , пересылаемых вдоль дуги 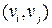, не может превышать пропускной способности этой дуги:

.

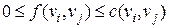Будем считать, что если существует дуга из вершины в вершину 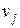, то нет дуги из вершины 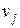в вершину . Таким образом, рассматривается поток вещества только в одну сторону.