 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм Дейкстры
|
|
Этап 1. Нахождение длины кратчайшего пути.
Шаг 1. Присвоение вершинам начальных меток.
Полагаем  , и считаем эту метку постоянной (постоянные метки помечаем сверху звездочкой). Для остальных вершин
, и считаем эту метку постоянной (постоянные метки помечаем сверху звездочкой). Для остальных вершин  ,
,  полагаем
полагаем  и считаем эти метки временными. Обозначим через
и считаем эти метки временными. Обозначим через  текущую вершину и примем первоначально
текущую вершину и примем первоначально  .
.
Шаг 2. Изменение меток.
Для каждой вершины  с временной меткой, непосредственно следующей за вершиной
с временной меткой, непосредственно следующей за вершиной  , меняем ее метку в соответствии со следующим правилом:
, меняем ее метку в соответствии со следующим правилом:
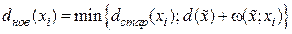 .
.
Шаг 3. Превращение временной метки в постоянную.
Из всех вершин с временными метками выбираем вершину  с наименьшим значением метки
с наименьшим значением метки
 где
где  − временная метка.
− временная метка.
Превращаем эту метку в постоянную и полагаем  .
.
Шаг 4. Проверка на завершение первого этапа.
Если  , то
, то  – длина кратчайшего пути от вершины
– длина кратчайшего пути от вершины 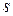 до
до  . В противном случае происходит возвращение ко второму шагу.
. В противном случае происходит возвращение ко второму шагу.
Этап 2. Построение кратчайшего пути.
Шаг 5. Последовательный поиск дуг кратчайшего пути.
Среди вершин, непосредственно предшествующих вершине  с постоянными метками, находим вершину
с постоянными метками, находим вершину  , удовлетворяющую соотношению
, удовлетворяющую соотношению
 .
.
Включаем дугу  в искомый путь и полагаем
в искомый путь и полагаем  .
.
Шаг 6. Проверка на завершение второго этапа.
Если  , то кратчайший путь найден – его образует последовательность дуг, полученных на пятом шаге и выстроенных в обратном порядке. В противном случае возвращаемся к пятому шагу.
, то кратчайший путь найден – его образует последовательность дуг, полученных на пятом шаге и выстроенных в обратном порядке. В противном случае возвращаемся к пятому шагу.
Пример 3.1. По заданной матрице весов

найти величину минимального пути и сам путь от вершины  до вершины
до вершины  с помощью алгоритма Дейкстры.
с помощью алгоритма Дейкстры.
Решение.
Чтобы найти величину минимального пути и сам путь от вершины  до вершины
до вершины  с помощью алгоритма Дейкстры, построим орграф, у которого к каждой дуге припишем ее вес.
с помощью алгоритма Дейкстры, построим орграф, у которого к каждой дуге припишем ее вес.

Этап 1. Шаг 1. Полагаем  ,
,
 .
.
Шаг 2. За вершиной  следуют вершины, которые образуют множество
следуют вершины, которые образуют множество  .
.
Пересчитаем временные метки:
 ,
,  ,
,
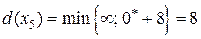 ,
,  .
.
Получаем  . Следовательно, вершине
. Следовательно, вершине  присваивается постоянная метка:
присваивается постоянная метка:  ,
,  .
.
Шаг 3.  . Пересчитаем временные метки:
. Пересчитаем временные метки:
 ,
,  ,
,
 ,
,  .
.
Получаем  . Следовательно, вершине
. Следовательно, вершине 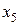 присваивается постоянная метка:
присваивается постоянная метка:  ,
,  .
.
Шаг 4.  . Пересчитаем временные метки:
. Пересчитаем временные метки:
 ,
,  ,
,
 ,
,  .
.
Получаем  . Следовательно, вершине
. Следовательно, вершине  присваивается постоянная метка:
присваивается постоянная метка: 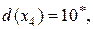
 .
.
Шаг 5.  . Пересчитаем временные метки:
. Пересчитаем временные метки:
 ,
,
 ,
,
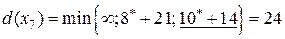 .
.
Получаем  . Следовательно, вершинам
. Следовательно, вершинам  и
и  присваиваются постоянные метки:
присваиваются постоянные метки: 


 .
.
Шаг 6.  . Вершине
. Вершине  присваивается постоянная метка
присваивается постоянная метка 
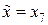 .
.
Этап 2.
Проводим последовательный поиск дуг кратчайшего пути.
Вершине 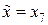 предшествуют вершины
предшествуют вершины  . Кратчайшее расстояние получим при прохождении по дуге
. Кратчайшее расстояние получим при прохождении по дуге 
Вершине  предшествуют вершины
предшествуют вершины  . Кратчайшее расстояние получием при прохождении по дуге
. Кратчайшее расстояние получием при прохождении по дуге 
Таким образом, кратчайший путь от вершины  до вершины
до вершины  построен. Его длина (вес) составляет 21, т.е.
построен. Его длина (вес) составляет 21, т.е.  , сам путь задает следующую последовательность дуг
, сам путь задает следующую последовательность дуг  –
– 
Ответ:  ,
,  –
– 
4. ЭЙЛЕРОВЫ И ГАМИЛЬТОНОВЫ ЦИКЛЫ
Дата публикования: 2014-10-19; Прочитано: 5240 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
