 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пути и циклы Эйлера
|
|
Выше были введены понятия «путь» и «цикл» для связного графа. Особый интерес представляют два цикла, имеющие практическое применение - эйлеров цикл и гамильтонов цикл.
Пусть 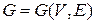 – граф.
– граф.
Определение 4.1. Цикл, который включает все ребра и вершины графа 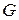 , называется эйлеровым циклом. Граф, в котором существует эйлеров цикл называется эйлеровым.
, называется эйлеровым циклом. Граф, в котором существует эйлеров цикл называется эйлеровым.
Эйлеров цикл содержит не только все ребра (каждое ребро включается в цикл только один раз), но и все вершины графа (каждая вершина может быть включена в цикл несколько раз). С эйлеровым циклом непосредственно связана задача о кенигсбергских мостах. Заметим, что эйлеровым может быть только связный граф, однако не в каждом случае.
Теорема 4.1 (Эйлера). Связный граф является эйлеровым тогда и только тогда, когда степень каждой его вершины четная.
Доказательство.
Необходимость. Пусть 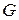 – связный эйлеров граф. Эйлеров цикл этого графа, проходя через каждую его вершину, входит в нее по одному ребру, а выходит по другому. Это означает, что каждое прохождение вершины по циклу добавляет в ее степень слагаемое 2. Поскольку цикл содержит все ребра графа, то степени всех вершин будут четными.
– связный эйлеров граф. Эйлеров цикл этого графа, проходя через каждую его вершину, входит в нее по одному ребру, а выходит по другому. Это означает, что каждое прохождение вершины по циклу добавляет в ее степень слагаемое 2. Поскольку цикл содержит все ребра графа, то степени всех вершин будут четными.
Достаточность.
Предположим, что степени всех вершин связного графа 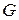 четные. Начнем цепь
четные. Начнем цепь  из произвольной вершины
из произвольной вершины 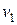 , и будем продлевать ее, выбирая каждый раз новое ребро. Так как степень каждой из вершин четная, то, попав в некоторую вершину, мы всегда будем иметь в распоряжении еще не пройденное ребро. Таким образом, построение цепи
, и будем продлевать ее, выбирая каждый раз новое ребро. Так как степень каждой из вершин четная, то, попав в некоторую вершину, мы всегда будем иметь в распоряжении еще не пройденное ребро. Таким образом, построение цепи  обязательно закончится в вершине
обязательно закончится в вершине 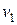 , и
, и  будет циклом. Если
будет циклом. Если  содержит все ребра графа
содержит все ребра графа 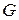 , то построен эйлеров цикл.
, то построен эйлеров цикл.
В противном случае, удалив из графа 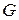 ребра цепи
ребра цепи  , получим граф
, получим граф  . Так как степень всех вершин графов
. Так как степень всех вершин графов 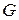 и цепи (графа)
и цепи (графа)  были четными, то и граф
были четными, то и граф  будет обладать этим свойством. В силу связности
будет обладать этим свойством. В силу связности 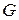 графы
графы  и
и  должны иметь хотя бы одну общую вершину
должны иметь хотя бы одну общую вершину  . Теперь начиная из
. Теперь начиная из  , построим в графе
, построим в графе 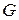 цикл
цикл  подобно тому, как построили
подобно тому, как построили  .
.
Объединим циклы  и
и  следующим образом: пройдем часть
следующим образом: пройдем часть  от вершины
от вершины 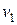 до вершины
до вершины  , затем пройдем цикл
, затем пройдем цикл  , затем – оставшуюся часть
, затем – оставшуюся часть  от
от  до
до 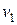 , рис. 4.1.
, рис. 4.1.
Если объединенный цикл не эйлеров, проделав аналогичные построения, получим еще больший цикл. Поскольку степени вершин во всех графах, составленных из ребер, не попавших в строящийся цикл, четные, и число ребер в этих графах убывает, то процесс закончится построением эйлерова цикла.

Рис. 4.1,
Заметим, что данная теорема справедлива также и для мультиграфов, и для псевдографов, исключая тот случай, когда псевдограф имеет только одну вершину.
Данная теорема служит критерием существования эйлерова цикла в графе. Это связано с тем, что эйлеровых графов с числом вершин 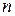 среди множества графов с тем же числом вершин почти нет. Можно отметить, что характерной особенностью эйлерова граф является то, что его можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.
среди множества графов с тем же числом вершин почти нет. Можно отметить, что характерной особенностью эйлерова граф является то, что его можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.
Заметим также, что теорема 4.1 позволяет аргументировать невозможность построения эйлерова цикла в задаче о кенигсбергских мостах: этот граф содержит все вершины нечетной степени.
С другой стороны, в данной задаче о кенигсбергских мостах можно было бы поставить и такой вопрос: «Возможно, ли пройти каждый мост по одному разу, но не обязательно возвращаться в исходную точку?» В связи с этим рассмотрим такие понятия как эйлеров путь и собственный эйлеров путь.
Пусть 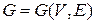 – граф.
– граф.
Определение 4.2. Путь, который включает каждое ребро графа 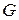 только один раз, называется эйлеровым путем. Эйлеров путь, который не является циклом, называется собственным эйлеровым путем.
только один раз, называется эйлеровым путем. Эйлеров путь, который не является циклом, называется собственным эйлеровым путем.
Теорема 4.2*. Граф (мультиграф или псевдограф) имеет собственный эйлеров путь тогда и только тогда, когда он связный и ровно две его вершины имеют нечетную степень.
Согласно этой теореме, задача о кенигсбергских мостах так же не имеет и эйлерова пути.
Аналогичным образом можно ввести понятие эйлерова цикла для ориентированного графа и условие существования эйлерова цикла в орграфе.
Пусть 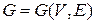 – ориентированный граф.
– ориентированный граф.
Определение 4.3. Ориентированный цикл, который включает все ребра и вершины графа 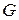 , называется эйлеровым циклом.
, называется эйлеровым циклом.
Теорема 4.3*. Ориентированный граф имеет эйлеров цикл тогда и только тогда, когда он связный и полустепень захода каждой вершины равна ее полустепени исхода.
Пример 4.1. Из какого минимального числа кусков проволоки можно спаять каркас куба? Толщина всех ребер каркаса должна быть одинаковой.
Решение.

Теорема 4.4*. Если связный граф содержит ровно  вершин нечетной степени, то минимальное число реберно-непересекающихся цепей, на которые можно разбить его ребра, равно
вершин нечетной степени, то минимальное число реберно-непересекающихся цепей, на которые можно разбить его ребра, равно 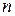 .
.
Дата публикования: 2014-10-19; Прочитано: 3366 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
