Алгоритм Прима

1. Выбрать вершину 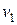графа 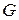и ребро с наименьшим весом , для которого 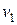– одна из вершин, и сформировать дерево .

2. Для заданного дерева с ребрами , при наличии вершины, не принадлежащей , следует выбрать ребро с наименьшим весом, смежное с ребром дерева и имеющее вершину вне дерева . Добавить новую вершину в дерево , формируя дерево .

3. Продолжать, пока имеются вершины графа 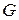, не принадлежащие дереву.

Построение минимального остовного дерева можно проводить двумя способами: 1) остов графа строится непосредственно на самом графе, выделяя ребра утолщенной линией, которые входят в остовное дерево; 2) отдельно строится корневое дерево, которое будет минимальным остовным деревом. Второй случай используется, если требуется определить высоту построенного дерева.

Пример 2.3. Для данного взвешенного графа:

1) определить степень каждой вершины;

2) построить матрицу смежности вершин, матрицу смежности ребер, матрицу инциденций;

3) найти минимальное корневое остовное дерево, используя алгоритм Краскала или алгоритм Прима.

Решение.

1) Используя определение степени вершины графа, находим:

, , , , .

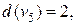
2) Построим матрицу смежности вершин. Данный граф имеет шесть вершин, поэтому матрица смежности вершин 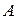является квадратной матрицей шестого порядка. Для заполнения первой строки матрицы 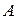найдем число ребер, соединяющих первую вершину с каждой из остальных вершин.

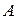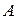Поскольку количество ребер, соединяющих первую вершину с первой равно нулю (в графе нет петель, соответствующих первой вершине), количество ребер соединяющих первую со второй равно одному, первую с третьей − одному, первую с четвертой − одному, первую с пятой − нулю, первую с шестой − нулю, то первая строка матрицы имеет вид . Заполняя аналогично остальные строки, получим матрицу вида:

.

Для построения матрицы смежности ребер и матрицы инциденций рассмотрим не взвешенный граф, предварительно занумеровав ребра графа произвольным образом.

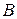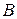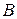Так как граф имеет девять ребер, то матрица смежности ребер является квадратной матрицей девятого порядка. Ребро имеет общую вершину сребрами и , а также общую вершину с ребрами и . Поэтому первая строка матрицы имеет вид . Заполняя аналогично остальные строки, получим матрицу вида:

.

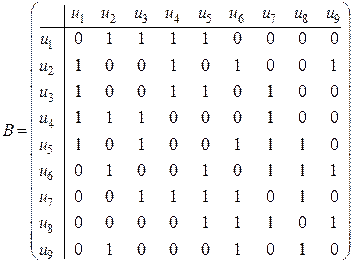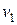Граф имеет шесть вершин и девять ребер, поэтому матрица инциденций имеет размерность . Поскольку вершина инцидентна ребрам и , и не инцидентна остальным ребрам, то первая строка матрицы имеет вид . Остальные строки матрицы заполняются аналогично. Следовательно, матрица будет иметь вид:

.

3) Для построения минимального остовного (корневого) дерева рассмотрим взвешенный граф, данный в условии задачи.

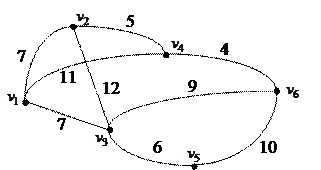
I способ. Используем для построения остовного дерева алгоритм Краскала. В графе выберем ребро с минимальным весом. В нашем случае это ребро, соединяющее вершины и с весом, равным 4. Пусть, например, вершина будет корнем дерева. Далее выбираем ребра, инцидентные вершинам , и имеющие минимальный вес. Таким будет ребро с весом 5, соединяющее вершины и . Включим его в строящееся дерево. Затем к вершине присоединим ребро с весом 7, соединяющее вершины и 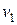. К вершине 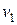присоединим ребро с весом 7, соединяющее вершины 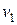и . И, в заключение, к вершине присоединим ребро с весом 6, соединяющее вершины и . Таким образом, получаем минимальное остовное дерево. Минимальный вес построенного дерева равен: .

Так как мы в качестве корня дерева выбрали вершину , то высота дерева будет равна .

Заметим, что если в качестве корня выбрать вершину , то высота дерева будет равна .

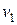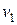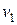II способ. Рассмотрим построение минимального корневого остовного дерева данного взвешенного графа с помощью алгоритма Прима. Выберем вершину , которая будет корнем дерева. Из трех ребер, которые инцидентны вершине , выберем те, что имеют наименьший вес. Два ребра с весом, равным , инцидентны вершине . Присоединим эти ребра к выбранной вершине. К вершине 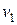присоединим ребро с весом , соединяющее вершины и . К вершине присоединим ребро с весом , соединяющее вершины и . К вершине присоединим ребро с весом , соединяющее вершины и . Таким образом, получаем следующее минимальное корневое дерево с весом, равным 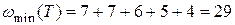. Заметим, что высота построенного дерева равна .

Ответ:

1) , , , , ;

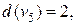
3) число остовных деревьев равно ;

4) минимальный вес дерева равен .

3. НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ. АЛГОРИТМ ДЕЙКСТРЫ

Остановимся на вопросе перемещения из одной вершины в другую с позиции «наилучшего способа» достижения оптимального значения определенного критерия. Детализируем это требование: это может быть как самый дешевый путь по стоимости, так и самый кратчайший путь по протяженности, как самый безопасный путь, так и наименее энергопотребляющий, и т.д.

Для решения такого класса задач рассматриваются взвешенные графы (орграфы), ребрам (дугам) которых приписан некоторый вес. Общий подход к решению задачи о кратчайшем пути был развит американским математиком Ричардом Беллманом (1920 – 1984), который предложил для этого вида задач название динамическое программирование. Задача о кратчайшем пути – это частный случай задачи, которую можно сформулировать следующим образом: найти в заданном графе пути, соединяющие две заданные вершины и доставляющие минимум или максимум некоторой аддитивной функции, определенной как критерий эффективности множества путей. Чаще всего эта функция трактуется как длина пути, и задача называется задачей о кратчайшем пути.

Алгоритм Дейкстры (Едсгер Дейкстра, нидерландский математик, 1930 – 2002) является одной из реализаций этой задачи. Данный алгоритм часто еще называют алгоритмом расстановки меток.

Пусть – ориентированный граф с взвешенными дугами. Обозначим через 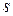( 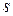-вершина) – вершину начала пути и через ( -вершину) – вершину конца пути. В процессе работы алгоритма Дейкстры вершинам орграфа приписываются числа (метки) , которые служат оценкой длины (веса) кратчайшего пути от 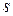-вершины к вершине . Если вершина получила на некотором шаге метку , это означает, что в графе 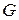существует путь из 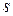-вершиныв , имеющий вес . Метки могут находиться в двух состояниях – быть временными или постоянными. Превращение временной метки в постоянную означает, что кратчайшее расстояние от вершины 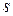до соответствующей вершины найдено. Алгоритм Дейкстры содержит одно ограничение – веса дуг должны быть положительными. Сам алгоритм состоит из двух этапов. На первом этапе находится длина кратчайшего пути, на втором − строится сам путь от вершины 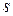к вершине .