Пример 2.1

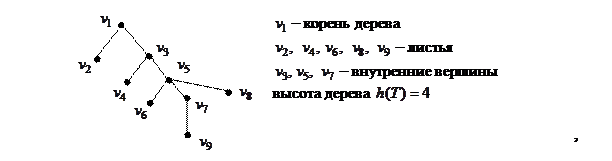
Рассмотрим некоторые утверждения, которые относятся к деревьям.

Теорема 2.1. Для любых вершин 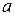и 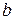дерева 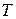существует единственная цепь из 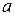в .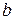

Доказательство.

Доказательство проведем методом «от противного». Предположим, что для некоторых вершин 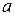и 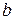дерева 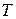цепь из 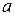в 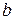не является единственной, и покажем, что в таком случае 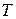не будет деревом.

Рис.2.1

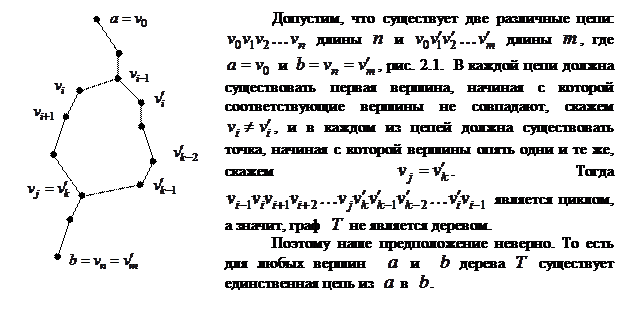
Верна также и обратная теорема.

Теорема 2.2*. Если для любых двух вершин графа 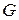существует единственная цепь из вершины 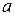в вершину 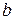, тогда 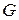является деревом.

Теорема 2.3. Если у дерева 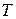имеется 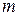ребер и 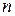вершин, то .

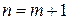Доказательство.

Предположим, что имеется дерево 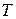. Любое дерево можно представить как корневое дерево, и это никаким образом не меняет ни числа ребер, ни числа вершин.

Рассмотрим теперь ориентированное дерево 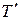, порожденное деревом 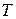. У каждой дуги ориентированного дерева одна и только одна конечная вершина. Следовательно, число дуг и вершин одно и то же, исключая корневую. Если учесть корневую вершину, получим, что вершин на одну больше, чем дуг.

Значит, и исходное дерево имеет число вершин на одну больше, чем число ребер.,

Справедлива также и обратная теорема.

Теорема 2.4*. Если в связном графе 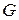, содержащем 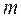ребер и 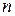вершин, выполнено равенство 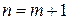, то граф 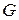является деревом.