Потери энергии в прыжке. Длина прыжка

Потери энергии (напора) в гидравлическом прыжке для прямоугольного русла, возможно найти из уравнения Бернулли и из уравнения (7.11) – оно следует из уравнения прыжка (7.7). Применяя уравнение Бернулли к сечениям до и после прыжка, получим

(7.13)

где - потери энергии в прыжке.

Так как 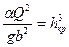, то из уравнения (7.13) найдем

(7.14)

Определив затем из (7.11)

,

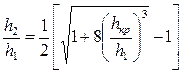и подставив в уравнение (7.14), получим формулу для определения потерь напора

(7.15)

Длина прыжка l может быть определена по формуле О.М. Айвазяна:

где

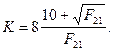
Задача 7.1. В канале трапецеидального сечения имеет место гидравлический прыжок. Определить вторую сопряженную глубину и критическую глубину при следующих данных: Q = 54,3 м³/с; b = 7,0 м; m = 1,0; h₁ = 0,8 м.

Указание. Вначале определяют критическую глубину графоаналитическим способом или подбором с помощью уравнения 5.2. Затем задают несколько глубин (2или 3) как больше критической, так и меньше критической глубины, определяют по ним значения прыжковой функции с помощью (7.8) и строят график прыжковой функции аналогично графику на рис. 7.4. По этому графику находят вторую сопряженную глубину, соответствующую первой сопряженной, которая задана (h₁=0,8м).Глубина погружения центра тяжести z под свободной поверхностью для живого сечения трапецеидальной формы определяется следующей формулой

,

где h – глубина потока, b – ширина по дну, m – коэффициент заложения откоса.

Ответ: h₂ = 3,13 м; h_кр =1,73 м.