Свойства прыжковой функции и ее график

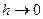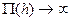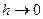В данном русле при постоянном расходе при прыжковая функция стремится к бесконечности, т.е. при ; при 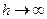также 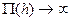. Прыжковая функция должна, следовательно, иметь минимум при некотором значении глубины.

Если найти производную 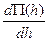и приравнять ее нулю, то определим, что прыжковая функция имеет минимальное значение при глубине, равной критической.

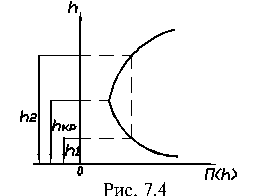
График прыжковой функции, построенный при заданных Q и

геометрических размерах поперечного сечения русла, рис 7.4. наглядно демонстрирует отмеченные особенности прыжковой функции.

Определение второй сопряженной глубины h₂ при заданной глубине h₁ производится непосредственно с помощью уравнения (7.7). Так, вычислив 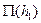, получим

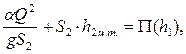
откуда и находим h₂ – аналитически или графическим путем с помощью построения графика прыжковой функции 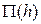, рис. 7.4. Построение этого графика производиться следующим образом: при расчетном расходе Q и известной форме поперечного сечения русла задаются рядом значений h и по уравнению

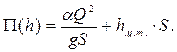
вычисляют соответствующие значения функции 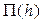. Далее, откладывая по оси ординат значения глубин h, а по оси абсцисс значения функции 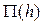, строят график прыжковой функции.

Сопряженные глубины h₁ и h₂ связаны между собой таким образом, что чем меньше h₁, тем больше h₂.

Из графика на рис. 7.4. видно, что в данном открытом русле при заданном расходе Q может быть большое число пар сопряженных глубин, но каждой заданной глубине h₁ перед прыжком соответствует только одна сопряженная с ней глубина h₂.