 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
В призматическом русле
|
|
При выводе основного уравнения гидравлического прыжка предполагаем, что прыжок происходит в вертикальной плоскости и движение плоское.
В качестве исходного применяем уравнение сохранения количества движения, это освобождает от необходимости учитывать потери механической энергии в области прыжка. По смыслу уравнения сохранения количества движения все силы, возникающие в отсеке жидкости внутри выделенной контрольной поверхности, принадлежат к силам внутренним и в уравнение не входят.
В прыжке возрастает глубина потока от значения h1 < hkр до значения h2 > hkр и соответственно площадь живого сечения от S1 до S2 (S2 > S1). Скорость течения, наоборот, уменьшается, т.е. V1 > V2; при этом, конечно
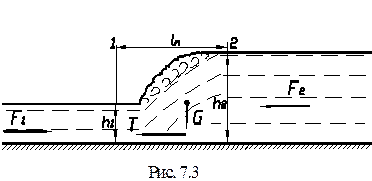 V1 S1 = V2 S2 = const = Q.
V1 S1 = V2 S2 = const = Q.
Cоставим уравнение сохранения количества движения массы жидкости, заключенной в объёме потока между сечением 1 с глубиной h1 и сечением 2 с глубиной h2, рис. 7.3; дно потока будем считать горизонтальным. Приращение количества движения 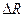 этой массы за единицу времени (в проекции на горизонтальную ось) равно
этой массы за единицу времени (в проекции на горизонтальную ось) равно
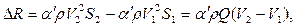
| (7.1) |
где 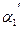 и
и 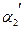 - коэффициенты количества движения.
- коэффициенты количества движения.
Внешними силами, вызывающими изменение количества движения являются: силы давления в сечениях 1 и 2 – F1 и F2, силы трения Fтр на внешней границе отсека и вес жидкости, заключенной в выделенном отсеке. В случае горизонтального дна проекция веса на направление движения равна нулю.
Примем следующие допущения:
1.Движение жидкости в сечениях 1 и 2 плавноизменяющееся, поэтому распределение давления в этих сечениях подчиняется гидростатическому закону;
2.Сила трения на границах отсека считается малой по сравнению с другими внешними силами, и ее не учитываем;
3.Коэффициенты количества движения в обоих сечениях принимаются одинаковыми, т.е. 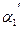 =
= 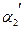 =
= 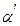 .
.
Тогда уравнение сохранения количества движения принимает вид
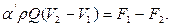
| (7.2) |
Исходя из гидростатического закона распределения давления в сечениях 1 и 2 получим
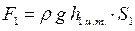 и и 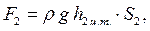
| (7.3) |
где h1.ц.т. и h2.ц.т – глубины погружения центров тяжести сечений 1 и 2, глубины в которых равны соответственно h1 и h2.
Имея в виду (7.3) зависимость (7.2) преобразуется к виду
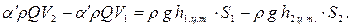
| (7.4) |
Учитывая, что 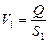 и
и 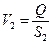
Левая часть (7.4) преобразуется к виду
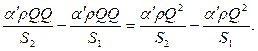
| (7.5) |
Уравнение (7.4) преобразуется к виду (после учёта (7.5) и деления левой и правой частей на 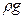 )
)
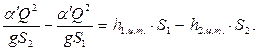
| (7.6) |
Группируя слагаемые, относящиеся к первому и второму сечениям в левой и правой частях соответственно, получим окончательный результат
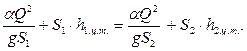
| (7.7) |
Это и есть основное уравнение гидравлического прыжка.
Так как S и hц.т. являются функциями глубины S=f(h) и 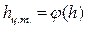 , а остальные величины постоянны, можно записать
, а остальные величины постоянны, можно записать
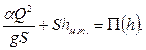
| (7.8) |
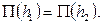
| (7.9) |
Функцию 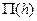 называют прыжковой функцией, и тогда уравнение (7.7) можно записать в кратной форме
называют прыжковой функцией, и тогда уравнение (7.7) можно записать в кратной форме
Дата публикования: 2014-10-25; Прочитано: 624 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
