Равномерное движение в открытых каналах

По аналогии с напорными потоками, равномерным движением в открытом русле будет такое установившееся движение, при котором в соответственных точках любых двух сечений скорости одинаковы по величине и по направлению, рис 2.1.

Равномерное движение в открытом русле может иметь место при следующих условиях:

1. Постоянство расхода воды .

2. Постоянство формы живого сечения и его геометрических характеристик (призматические каналы).

3. Постоянство геометрического уклона по всей длине канала .

4. Постоянство шероховатости русла и отсутствие местных сопротивлений.

Эти условия являются необходимыми, однако их недостаточно для того, чтобы в канале имело место равномерное течение; для этого необходимо также, чтобы глубина была одинакова во всех сечениях. Следствием того, что будет равенство уклона свободной поверхности уклону дна и гидравлическому уклону

.

Глубина потока h₀, соответствующая равномерному движению называется нормальной глубиной. Равномерное движение жидкости невозможно в естественных руслах, так как вдоль них практически все условия равномерного движения нарушаются.

Применим к двум сечениям, как на рис. 2.1 уравнение Бернулли с учётом потерь, тогда

, (2.1)

где l – расстояние между сечениями 1 и 2. Движущей силой при течении жидкости в открытом канале является сила тяжести и как следует из (2.1) при этом потенциальная энергия положения преобразуется в кинетическую энергию, которая ввиду существования сил трения преобразуется в тепло. Потери удельной энергии в открытом потоке при равномерном режиме легко определить из (2.1), но для расчётов это уравнение не может быть полезным, так как в него не входят ни расход, ни геометрические параметры сечения.

Для гидравлических расчётов равномерных потоков применяется формула Шези

, (2.2)

где Q – расход воды, C – коэффициент Шези, S – площадь поперечного сечения, R – гидравлический радиус, i – уклон дна. Формула Шези применяется при расчётах равномерных потоков и при этом , поэтому вместо часто пишется просто .

Для определения коэффициента Шези С существует несколько эмпирических формул. Все они получены из опытов над течением воды в каналах с различной степенью шероховатости при различных уклонах дна и различных скоростях течения. Считается экспериментально доказанным, что при квадратичном сопротивлении

,

где R – гидравлический радиус, n – коэффициент шероховатости стенок русла.

Представим себе открытый (безнапорный) равномерный поток с гладкой (без волн) свободной поверхностью. Ничего не изменится, если его сверху накрыть абсолютно твердой пластиной, не создающей трения на свободной поверхности этого потока – таким образом будет выполнено условие непротекания и рассматриваемый открытый поток можно будет считать напорным. Формула связывает коэффициент Шези с с коэффициентом гидравлического трения λ и общефункциональная зависимость коэффициента λ от и Rе, установленная для напорных потоков переходит на потоки безнапорные. Так как в данном случае напорного потока зависимости сопротивления от числа Фруда нет, то и для безнапорного (открытого) потока с гладкой (без волн) свободной поверхностью зависимости сопротивления от числа Фруда не существует (физический смысл числа Фруда изложен, в частности, в 9.2).

Так как обычно живые сечения открытых каналов по своим размерам больше сечений напорных труб, то и число Рейнольдса в них обычно велико. В то же время величина абсолютной шероховатости стенок открытых каналов больше, чем у труб и относительная шероховатость также остается большой. В результате движение в открытых каналах в большинстве случаев происходит в режиме квадратичного сопротивления и величина коэффициента Шези С зависит только от шероховатости стенок канала.

Все формулы для С справедливы в квадратичной области, и зависимость от числа Рейнольдса в них отсутствует; все они дают близкие между собой значения для С. Размерность коэффициента С такая

.

Ниже приводятся некоторые наиболее употребительные зависимости для С. Заметим, что размерности левых и правых частей этих зависимостей не совпадают, что является признаком их эмпирического происхождения.

1. Формула Маннинга (1890г.)

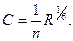(2.3)

2. Формула И.И.Агроскина (1949г.)

(2.4)

3. Формула Н.Н.Павловского ()

(2.5)

где (2.6)

4. Формула Н.Н.Павловского в сокращённом варианте

(2.7)

где при и при .

Во всех этих формулах приняты следующие обозначения: R – гидравлический радиус, n – коэффициент шероховатости, зависящий от рода стенки и определяемый по таблицам. Например, для бетонированных стенок в средних условиях , при грубой бетонировке стенок . В открытых руслах, как правило, наблюдается турбулентный режим движения; пример ламинарного течения, поддающегося точному расчёту, приведён в (Основные уравнения динамики жидкости, часть 3).

В гидравлических расчётах каналов применяют также расходную характеристику K

(2.8)

при этом

(2.9)

Это удобно тем, что из (2.9) следует

и в левой части отсутствует зависимость от каких-либо геометрических параметров сечения русла, в частности от глубины

Задача 2.1. Вывести формулу Шези (2.2) из формулы Дарси-Вейсбаха

Решение. Разделив обе части формулы Дарси-Вейсбаха на l – длину рассматриваемого участка, получим

(2.10)

Обычно принимают, что , где d – диаметр трубы, а в данном случае характерный размер канала, R – гидравлический радиус. Тогда из (2.10) следует

или

Окончательно формула Шези принимает вид

где принято обозначение

Задача 2.2. Вывести уравнение равномерного движения жидкости в открытом канале.

Решение. Равномерное движение возможно лишь в том случае, когда результирующая сила, действующая на любую частицу или фиксированный объем жидкости равна нулю. Движущей силой в открытом потоке является сила тяжести, а противодействующей ей при движении сила трения; в данном случае они равны. Если равнодействующая сила равна нулю, то равна нулю её проекция на любые направления; удобно в данном случае выбрать ось, совпадающую с направлением движения потока.Котсеку длиной L приложены силы: вес жидкости G = S∙L∙ρ∙g и сила сопротивления Т = τ_ст∙χ∙L, где S – площадь сечения потока, ρ - плотность жидкости, χ – смоченный периметр сечения, τ_ст – среднеекасательное напряжение на поверхности отсека. Силы давления F₁ в сечении 1 и F₂ в сечении 2 равны между собой, направлены противоположно и их динамический эффект равен нулю. Тогда в проекции на ось канала получаем уравнение

или ,

где R – гидравлический радиус, i – уклон дна канала.

3.Задачи расчёта равномерного движения в открытых руслах

Методика гидравлического расчёта параметров равномерного движения в открытых каналах любых форм сечений одинакова. Обычно рассматривается течение воды в каналах и основной расчётной зависимостью является формула Шези; принято различать три основных задачи по расчёту открытых каналов.