Инвестиции в В 4 страница

4. Компания владеет тремя спортивными центрами в деловой части города. На Пасху популярны велосипедные прогулки на открытом воздухе. В компании имеется восемь велосипедов, которые она может распределить между тремя центрами для их проката, чтобы максимизировать доходы. Спрос на велоси­педы и часовая стоимость их аренды зависят от месторасположения центра и характеризуются следующими данными.

Глава 15. Вероятностное динамическое программирование

Вероятность спроса
Количество велосипедов	Центр 1	Центр 2	Центр 3
	0,10	0,02
	, 0,20	0,03	0,15
	0,30	0,10	0,25
	0,20	0,25	0,30
	0,10	0,30	0,15
	0,10	0,15	0,10
		0,05	0,025
		0,05	0,025
		0,05
Арендная плата (долл./ч)

Как компании распределить восемь велосипедов между тремя спортивными центрами?

15.3. МАКСИМИЗАЦИЯ ВЕРОЯТНОСТИ ДОСТИЖЕНИЯ ЦЕЛИ

В разделе 15.2 рассматривалась задача, связанная с максимизацией ожи­даемой прибыли. Иным полезным критерием для рассмотренной задачи явля­ется максимизация вероятности достижения определенного уровня дохода. Продемонстрируем этот подход на примере модели инвестирования, которая описана в разделе 15.2.

Используя обозначения из раздела 15.2, оставим без изменения определение этапа i, альтернативы y_t и состояния х_г Эти модели отличаются только опреде­лением критерия; здесь нашей целью является максимизация вероятности дости­жения некоторой накопленной денежной суммы S по истечении п лет. С этой точки зрения определим функцию f_t(x) — вероятность накопления суммы S, если в нача­ле i-ro года имеются денежные средства в сумме х₁ и для последующих лет i, i +

п используется оптимальное инвестирование.

Рекуррентное уравнение динамического программирования имеет вид

f,{x,)= max \ ]ГpJ,_A (х, + r_ky>) I, / = 1,2,...,/»-1. Рекуррентная формула основана на формуле условной вероятности

Р{А}=£Р{А\В,}Р{В,}. В нашем случае + г_ку) играет роль вероятности Р{А | В^.

15.3. Максимизация вероятности достижения цели 603

Пример 15.3.1

Некий индивидуум планирует инвестировать 2 ООО долл. Имеющиеся варианты позволяют удвоить эту сумму с вероятностью 0,3 или потерять ее с вероятностью 0,7. Акции продаются в конце года, а в начале следующего года все деньги или их часть снова инвестируются. Этот процесс повторяется на протяжении трех лет. Целью является максимизация вероятности достижения суммы в 4 ООО долл. в конце третьего года.

В соответствии с обозначениями данной модели имеем г, = 1 с вероятностью 0,3 иг₂ = -1 с вероятностью 0,7.

Этап 3. На этом этапе состояние х₃ может изменяться от 0 до 8 000 долл. Ми­нимальное значение возможно, когда все вложенные средства потеряны, а максимальное — когда инвестиция удваивается в конце каждого из двух первых лет. Следовательно, рекуррентное уравнение для этапа 3 записывает­ся в следующем виде:

гдех₃ = 0,1,8.

Приведенная ниже табл. 15.1 содержит детали вычислений для данного этапа.

Все заштрихованные ячейки таблицы являются неподходящими, так как не удовлетворяют условию у_ъ < х₃. Кроме того, при выполнении вычислений можно за­метить, что

Р{х₃ + У₃ 2:4} = 0, если х₃ + у₃ < 4, Р{х₃ - у₃ > 4} = 0, если х₃ -у₃ < 4. В противном случае эти вероятности равны 1.

Хотя приведенная таблица и свидетельствует о том, что существуют альтерна­тивные оптимумы для х, = 1, 3, 4, 5, 6, 7 и 8, оптимальный (последний) столбец содержит лишь наименьшие оптимальные значения у₃. Это объясняется тем, что инвестор не собирается инвестировать больше того, что необходимо для достижения поставленной цели.

/₃(х,)= max

Г! =0,1.....*,

{0,ЗР{лг_3+>>₃>4} + 0,7/>{лг₃-_Л>4}},

Этап 2.

{0,3/₎(х_{2 + Л}) + 0,7/,(х₁-_Л)}.

Соответствующие вычисления приведены в табл. 15.2

Этап 1.

В табл. 15.3 показаны вычисления для данного этапа.

Таблица 15.1

	0,ЗР{Хз + уз > 4} + 0,7Р{хз - Уз £ 4}								Оптимум
Хз	Уз = 0 уз = 1	уз = 2	Уз = 3	Уз = 4	Уз = 5	Уз = 6	Уз = 7	Уз = 8		h	Уз
	0,3 х 0 + 0,7 х х0 = 0
	0,3х0 + 0,7х 0,3x0 + 0,7 х х 0 = 0 > 0 = 0
	0,3 х 0 + 0,7 х 0 3*0 + 07* х 0 = 0 v 0 = 0	0 3/1*07* * 0 = 0 3								0,3
	0,3x0 +0,7 х и,3х 1 +0,7х х 0 = 0 х 0 = 0,3	0,3 х 1 + 0,7 х х 0 = 0,3	0,3 х 1 +0,7 х х 0 = 0,3							0,3
	0,3 х 1 +0,7 х 0,3 х 1 +0,7х х1 = 1 х 0 = 0,3	0,3 х 1 + 0,7 х х 0 = 0,3	0,3х1 + 0,7х х 0 = 0,3	0,3 х 1 + 0,7 х х 0 = 0,3						1
	0,3 х 1 + 0,7 х 0,3 х 1 + 0,7 х X 1 = 1 X 1 = 1	0,3 х 1 + 0,7 х х0 = 0,3	0,3 х 1 + 0,7 х х 0 = 0,3	0,3 х 1 + 0,7 х х0 = 0,3	0,3 х 1 + 0 7 х х 0 = 0,3					1
	0,3 х 1 + 0,7 х 0,3 х 1 + 0,7 х X 1 = 1 X 1 = 1	0,3 х 1 + 0,7 х х 1 = 1	0,3 х 1 + 0,7 х х 0 = 0,3	0,3 х 1 + 0,7 х х 0 = 0,3	0,3x1 + 0,7/ х0 = 0,3	0 3-1+07 < 0 = 0.3	х^^^^^^Я			1
	0,3 х 1 + 0,7 х 0,3 х 1 + 0,7 х X 1 =1 X 1 =1	0,3 х 1 + 0,7 х х1 =1	0,3 х 1 + 0,7 х х 1 = 1	0,3 х 1 + 0,7 х х 0 = 0,3	0,3 х 1 + 0,7 х х 0 = 0,3	0,3 х 1 + 0,7 х 0 = 0,3	х 0,3 х 1 + 0,7 х х 0 = 0,3	Шт		1
	0,3 х 1 + 0,7 х 0,3 х 1 + 0,7 х X 1 = 1 X 1 = 1	0,3 х 1 + 0,7 х х1 = 1	0,3 х 1 + 0,7 х X 1 = 1	0,3 х 1 + 0,7 х X 1 = 1	0,3 х 1 + 0,7 х х0 = 0,3	0,3 х 1 + 0,7 х 0,3 х 1 + 0,7 х х 0 = 0,3 х 0 = 0,3	0,3 х х0 =	1 +0,7х 0,3	1
Таблица 15.2
	0,3f3(x2 + у2) + 0,7/з(Х2 - у2)								Оптимум
х2	у2 = 0 у 2 -	= 1	у2 = 2		У2 = 3		у2 = 4		h		Уг
	0,3 х 0 + 0,7 х 0 = 0								1°
	0,3 х 0 + 0,7 х 0 = 0	х 0,3 + 0,7 х 0	= 0,09 дИ			Elllllllllliille			"0,09
	0,3 х 0,3 + 0,7 х 0,3 = 0,3	х 0,3 + 0,7 х 0	= 0,09 0,3 х 1 + 0,7 х 0 = 0,3					§0,30
	0,3 х 0,3 + 0,7 х 0,3 = 0,3 u,J	х 1 + и,/ х и,а	= и.ап и,з х 1	+ и,/ хи = и,а	U.3X1 + и,/	х и = u,;s			0,51
	0,3 х 1 + 0,7 х 1 = 1 0,3	х 1 + 0,7 х 0,3	= 0,51 0,3 х 1 + 0,7 х 0,3 = 0,51 0,3 х 1 + 0,7 х 0 = 0,3	0,3 х 1 + 0,7 х 0	= 0,3

Литература 605

Таблица 15.3

	О.З/гОо + У\) + QJh(x\ - у{) Оптимум
	У\ = 0 у, = 1 у, = 2 fi Xi
	0,3x 0,3 + 0,7 x 0,3 = 0,3 0,3 x 0,51 + 0,7 x 0,09 = 0,216 0,3 x 1 +0,7 x0 = 0,3 0,3 0

Оптимальная стратегия определяется следующим образом. При заданной начальной сумме х, = 2000 долл. вычисления для первого этапа дают у_г = 0. Это означает, что в первый год не следует делать инвестиций. Данное решение оставляет инвестора с 2000 долл. к началу второго года. Из таблицы, соответствующей второму этапу, при х₂ = 2 получаем у_г = 0; это снова означает, что на протяжении второго года также не следует делать инвестиций. Далее использование значения х₃ = 2 на третьем этапе приводит ку_ъ = 2, а это означает, что на третий год следует инвестировать всю имею­щуюся в распоряжении сумму. Соответствующая максимальная вероятность дости­жения цели 5=4 равна/,(2) = 0,3.

УПРАЖНЕНИЯ 15.3

1. В примере 15.3.1 этап 1 решения задачи показывает, что существует два аль­тернативных оптимума: у₁ = 0 и у, = 2. Покажите, что применение стратегии у, = 2 (т.е. инвестировать все деньги в начале первого года) не изменяет резуль­тата инвестиционной политики на протяжении трех лет, а именно, соответст­вующая максимальная вероятность достижения цели сохраняется равной 0,3.

2. Решите задачу из примера 15.3.1, если целью инвестора является максими­зация вероятности достижения по меньшей мере суммы в 6 000 долл. к кон­цу третьего года. Инвестор имеет в своем распоряжении 1000 долл., и веро­ятность удвоения суммы на протяжении каждого года равна 0,6.

3. Вы и ваш друг хотите сыграть в казино в следующую игру. Вы делаете опреде­ленную ставку, и каждый из вас независимо подбрасывает симметричную мо­нету. За каждый доллар суммы ставки казино заплатит три доллара (что дает чистую прибыль в 2 долл.), если в результате подбрасывания выпадут две реш­ки. Иначе вы теряете сумму ставки. Если вы с другом имеете в сумме один дол­лар, определите стратегию игры, считая, что целью является максимизация вероятности окончания трех игр с суммой в 4 долл.

ЛИТЕРАТУРА

1. Bertsekas D. Dynamic Programming: Deterministic and Stochastic Models, Pren­tice Hall, Upper Saddle River, N. J., 1987.

2. Cooper L. and Cooper M. Introduction to Dynamic Programming, Pergamon Press, New York, 1981.

3. Smith D. Dynamic Programming: A Practical Introduction, Ellis Horwood, Lon­don, 1991.

Литература, добавленная при переводе

1. Беллман Р., Дрейфус С. Прикладные задачи динамического программирова­ния. — М.: Наука, 1965.

2. Романовский И. В. Алгоритмы решения экстремальных задач. — М.: Наука, 1977.

Глава 15. Вероятностное динамическое программирование

КОМПЛЕКСНАЯ ЗАДАЧА

15.1. Компания использует грузовые автомобили для доставки заказов покупате­лям и планирует заменить свои автомобили на прРяжении последующих пяти лет. Годовые затраты, связанные с использованием нового грузовика, являются нормально распределенной случайной величиной с математиче­ским ожиданием 300 долл. и среднеквадратическим отклонением 50 долл. Математическое ожидание и среднеквадратическое отклонение годовых эксплуатационных затрат через год возрастают на 10 %. Стоимость нового грузового автомобиля в настоящее время равна 20 000 долл. и через год воз­растет, как ожидается, на 12 %. Грузовые автомобили используются чрез­вычайно интенсивно, поэтому существует вероятность того, что каждый из них может окончательно сломаться в любое время. Можно сдать старый ав­томобиль при покупке нового. При этом стоимость старого автомобиля за­висит от того, находится ли он в рабочем состоянии. В начале шестого года автомобиль подлежит продаже по цене, которая также зависит от его со­стояния (аварийное или рабочее). Приведенная ниже таблица содержит данные, описывающие ситуацию в зависимости от возраста автомобиля.

Возраст автомобиля (годы)	0 1 2 3 4 5 6
Вероятность поломки	0,01 0,05 0,10 0,16 0,25 0,40 0,60

Если автомобиль использовался 1 год и находится в рабочем состоянии, то его стоимость равна 70 % от начальной и за год уменьшается на 15 %. Если же он находится в аварийном состоянии, то соответствующие показатели уменьшаются в два раза. Стоимость автомобиля в виде испорченного иму­щества в начале шестого года составляет 200 долл., если он находится в ра­бочем состоянии, и 50 долл., если он аварийный. Разработайте оптималь­ную политику замены автомобилей.

ГЛАВА 16

ВЕРОЯТНОСТНЫЕ МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ

В главе 11 изложены основы теории управления запасами в условиях определенно­сти¹. В этой главе рассматриваются вероятностные модели управления запасами, в которых значение спроса является случайной величиной с известным распределением вероятностей. Рассмотренные модели подразделяются на модели с непрерывным и на модели с периодическим контролем уровня запаса. При этом класс моделей с периоди­ческим контролем включает как одноэтапные, так и многоэтапные модели.

16.1. МОДЕЛЬ С НЕПРЕРЫВНЫМ КОНТРОЛЕМ УРОВНЯ ЗАПАСА

В этом разделе рассмотрены две модели управления запасами: 1) обобщение де­терминированной модели экономичного размера заказа (см. раздел 11.2.1) на вероят­ностный случай, в которой используется буферный запас, отвечающий за случайный спрос и 2) более точная вероятностная модель экономичного размера заказа, которая учитывает вероятностный характер спроса непосредственно в постановке задачи.

16.1.1. "Рандомизированная" модель экономичного размера заказа

Некоторые специалисты пытались адаптировать детерминированную модель эко­номичного размера заказа (см. раздел 11.2.1) для учета вероятностной природы спро­са, используя при этом приближенный метод, который предполагает существование постоянного буферного запаса на протяжении всего планового периода. Размер ре­зерва устанавливается таким образом, чтобы вероятность истощения запаса в течение периода выполнения заказа (интервала между моментом размещения заказа и его по­ставкой) не превышала наперед заданной величины.

Введем следующие обозначения.

L — срок выполнения заказа, т.е. время от момента размещения заказа до его поставки,

х_ь — случайная величина, представляющая величину спроса на протяжении срока выполнения заказа,

p:_L — средняя величина спроса на протяжении срока выполнения заказа,

¹ Данная глава продолжает тему главы 11, посвященной детерминированным моделям управления запасами.

Глава 16. Вероятностные модели управления запасами

<7_L — среднеквадратическое отклонение величины спроса на протяжении срока выполнения заказа,

В — размер резервного запаса,

а— максимально возможное значение вероятности истощения запаса на про­тяжении срока выполнения заказа.

Основным предположением при построении модели является то, что величина спроса х_ь на протяжении срока выполнения заказа L является нормально распре­деленной случайной величиной со средним fi_L и стандартным отклонением a_L, т.е. имеет распределение N(fi_L,cr_L).

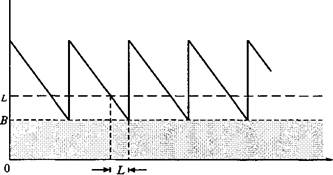
На рис. 16.1 показана зависимость между размером резервного запаса В и пара­метрами детерминированной модели экономичного размера заказа, которая включа­ет срок выполнения заказа L, среднюю величину спроса ц_ь на протяжении срока вы­полнения заказа и экономичный размер заказа у. Заметим, что L должно быть равно эффективному времени выполнения заказа, как это определено в разделе 11.2.1.

Уровень I запаса

В + у

В + V

Время

Рис. 16.1. Резервный запас в детерминированной модели экономич­ного размера заказа

Вероятностное условие, которое определяет размер резервного запаса В, имеет вид

P/x_L>B + \xj <а. По определению (см. раздел 12.4.4) случайная величина

является стандартной нормально распределенной случайной величиной, т.е. имеет распределение ЛГ(0, 1). Следовательно,

P\z>

В

На рис. 16.2 показана величина К_а, которая определяется из таблицы стандарт­ного нормального распределения (см. приложение В), так что

P/z >KJ = a.

Следовательно, размер резервного запаса должен удовлетворять неравенству

B>o_LK,r

16.1. Модель с непрерывным контролем уровня запаса

N(0, 1)

/

Площадь = о

z

Рис. 16.2. Определение вероятности P/z >К_а/ - а

Величина спроса на протяжении срока выполнения заказа L обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно найти распределение спроса на протяжении пе­риода L. В частности, если спрос за единицу времени является нормально распределен­ной случайной величиной со средним D и стандартным отклонением о, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(jj_l, a_L), где /j, = DL и о, = -Vg²/.. Формула для a_L получена на основании того, что значение L является целым числом (или же округлено до целого числа).

Пример 16.1.1

В примере 11.2.1, где речь шла об управлении запасом неоновых ламп в универ­ситетском городке, был определен экономичный размер заказа в 1000 ламп. Тре­буется определить размер резервного запаса таким образом, чтобы вероятность истощения запаса не превышала а = 0,05 при условии, что дневной спрос являет­ся нормально распределенной случайной величиной с математическим ожидани­ем D=100 ламп и среднеквадратическим отклонением о= 10 ламп, т.е. имеет распределение yV(100, 10).

Как следует из примера 11.2.1, эффективное время выполнения заказа L равно 2 дня. Следовательно,

Из таблицы стандартного нормального распределения (приложение В) опреде­ляем ^0,05 = 1,645. Следовательно, размер резервного запаса вычисляется сле­дующим образом.

При экономичном размере заказа у* = 1000 единиц оптимальная политика управ­ления запасами с объемом резерва В состоит в заказе 1000 ламп, как только объем запаса уменьшается до 223 единиц (= В + ju_L = 23 + 2 х 100).

щ_ = DL = 100 х 2 = 200 единиц,

единиц.

В > 14,14 х 1,645 = 23 лампы.

Глава 16. Вероятностные модели управления запасами

УПРАЖНЕНИЯ 16.1.1

1. В примере 16.1.1 определите оптимальное управление запасами для каждого из следующих случаев.

a) Время выполнения заказа равно 15 дней.

b) Время выполнения заказа равно 23 дня.

c) Время выполнения заказа равно 8 дней.

d) Время выполнения заказа равно 10 дней.

2. Музыкальный магазин продает популярный компакт-диск. Распределение дневного спроса на диск можно аппроксимировать нормальным распределени­ем с математическим ожиданием 200 дисков и стандартным отклонением 20 дисков. Стоимость хранения диска в магазине составляет 0,04 долл. за один день. Размещение нового заказа обходится магазину в 100 долл. Поставщик обычно устанавливает семидневный срок для выполнения заказа. Предполо­жим, что магазин хочет ограничить вероятность истощения запаса дисков на протяжении срока выполнения заказа величиной, не превышающей 0,02. Оп­ределите оптимальное управление запасами для магазина.

3. Дневной спрос на фотопленку в подарочном магазине курортной зоны является нормально распределенной случайной величиной с математическим ожидани­ем 30 пленок и стандартным отклонением 5 пленок. Стоимость хранения ка­тушки с пленкой в магазине составляет 0,02 долл. Размещение нового заказа на фотопленку каждый раз обходится магазину в 30 долл. Стратегия магазина по управлению запасами состоит в размещении заказа на 150 фотопленок, как только уровень запаса опускается до 80 единиц, тем самым поддерживается одновременно постоянный резерв в 20 фотопленок.

a) Для указанной стратегии магазина по управлению запасами определите ве­роятность истощения запаса на протяжении срока выполнения заказа.

b) Разработайте рекомендации для магазина относительно стратегии по управлению запасами, предполагая, что вероятность истощения запаса пленок на протяжении срока выполнения заказа не превышает 0,10.

16.1.2. Стохастический вариант модели экономичного размера заказа

Нет оснований полагать, что "рандомизированная" модель экономичного раз­мера заказа, рассмотренная в разделе 16.1.1, определит оптимальную политику управления запасами. Подтверждением этого является то, что существенная ин­формация, имеющая отношение к вероятностной природе спроса, при этом подходе первоначально не учитывается, а используется лишь независимо на последнем эта­пе вычислений. Чтобы исправить такую "нездоровую" ситуацию, в этом разделе рассматривается более точная модель, в которой вероятностная природа спроса учитывается непосредственно в постановке задачи.

В отличие от ситуации, рассмотренной в разделе 16.1.1, в новой модели допус­кается неудовлетворенный спрос, как это показано на рис. 16.3. В рассматриваемой модели заказ размером у размещается тогда, когда объем запаса достигает уровня R. Как и в детерминированном варианте, уровень R, при котором снова размещает­ся заказ, является функцией периода времени между размещением заказа и его выполнением. Оптимальные значения у и R определяются путем минимизации ожидаемых затрат системы управления запасами, отнесенных к единице времени, которые включают как расходы на размещение заказа и его хранение, так и поте­ри, связанные с неудовлетворенным спросом.

16.1. Модель с непрерывным контролем уровня запаса 611

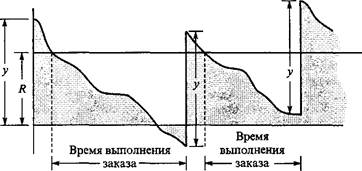
|-«-Цикл 1-*\*-Цикл 2-^

Рис. 16.3. Стохастическая модель экономичного размера заказа

В рассматриваемой модели приняты три условия.

1. Неудовлетворенный в течение срока выполнения заказа спрос накапливается.

2. Разрешается не более одного невыполненного заказа.

3. Распределение спроса в течение срока выполнения заказа является стацио­нарным (неизменным) во времени.

Для определения функции, отражающей суммарные затраты, отнесенные к единице времени, введем следующие обозначения.

f(x) — плотность распределения спроса х в течение срока выполнения заказа, D — ожидаемое значение спроса в единицу времени,

h — удельные затраты на хранение (на единицу продукции за единицу времени),

р — удельные потери от неудовлетворенного спроса (на единицу продукции за единицу времени),

К — стоимость размещения заказа.

Основываясь на этих определениях, вычислим компоненты функции затрат.

1. Стоимость размещения заказов. Приближенное число заказов в единицу времени равно D/y, так что стоимость размещения заказов в единицу време­ни равна KD/y.

2. Ожидаемые затраты на хранение. Средний уровень запаса равен

С_{У +} М_{Л-х)) ₊ М_{*-х_1ду 2 2

Следовательно, ожидаемые затраты на хранение за единицу времени равны hi.

Приведенная формула получена в результате усреднения ожидаемых запасов в начале и конце временного цикла, т.е. величин y + M{R-x) и M{R-x} со­ответственно. При этом игнорируется случай, когда величина R -М{х) мо­жет быть отрицательной, что является одним из упрощающих допущений рассматриваемой модели.

Глава 16. Вероятностные модели управления запасами

3. Ожидаемые потери, связанные с неудовлетворенным спросом. Дефицит возни­кает при х > R. Следовательно, ожидаемый дефицит за единицу времени равен

S = ](x-R)f{x)dx.

к

Так как в модели предполагается, что р пропорционально лишь объему дефици­та, ожидаемые потери, связанные с неудовлетворенным спросом, за один цикл рав­ны pS. Поскольку единица времени содержит D/y циклов, то ожидаемые потери, обусловленные дефицитом, составляютpDS/y за единицу времени.

Результирующая функция общих потерь за единицу времени TCU имеет сле­дующий вид.

TCU(y, R)^^ + h[^ + R~M{x]\_j + ^-"\{x-R)f{x)dx.

Оптимальные значения у* и R* определяются из представленных ниже уравнений.

3TCU _ (DK) h _PD — -{~}⁺2-—^S-°'

^-*-(f)I'^w*-^ft

Следовательно, имеем

2D(K + pS)

⁽²⁾

Так как из уравнений (1) и (2) у* и R нельзя определить в явном виде, для их по­иска используется численный алгоритм, предложенный Хедли и Уайтин (Hadley, Whitin) [1]. Доказано, что алгоритм сходится за конечное число итераций при ус­ловии, что допустимое решение существует.

При R = О последние два уравнения соответственно дают следующее.

\ 2Р{К + р М{х})

Если у > у, тогда существуют единственные оптимальные значения для у и R. Вы­числительная процедура определяет, что наименьшим значением у" является \J2KDIh, которое достигается при S = 0.

Алгоритм состоит из следующих шагов.

ШагО. Принимаем начальное решение у, = у' = ^2KD/h и считаем R₀ = 0.

Полагаем i = 1 и переходим к шагу i.

Шаг i. Используем значение у. для определения Д, из уравнения (2). Ес­ли Д, = Д,^, вычисления заканчиваются; оптимальным решением считаем у = у, и R' = Д,. Иначе подставляем значение Д, в уравне­ние (1) для вычисления у_г Полагаем i = i + 1 и повторяем шаг i.

16.1. Модель с непрерывным контролем уровня запаса

Пример 16.1.2

Электротехническая компания использует в производственном процессе канифоль в количестве 1000 галлонов в месяц. Размещение заказа на новую поставку канифоли об­ходится фирме в 100 долл. Стоимость хранения одного галлона канифоли на протя­жении одного месяца равна 2 долл., а удельные потери от ее дефицита — 10 долл. за один галлон. Статистические данные свидетельствуют о том, что спрос в период по­ставки является случайной величиной, равномерно распределенной от 0 до 100 гал­лонов. Надо определить оптимальную политику управления запасами для компании.

Используя принятые в модели обозначения, имеем следующее.

D = 1000 галлонов в месяц,

К = 100 долл. за размещение заказа,

/(= 2 долл. за один галлон в месяц,

р = 10 долл. за один галлон,

Дх)= 1/100, 0<х< 100,

М{х) = 50 галлонов.

Сначала необходимо проверить, существует ли допустимое решение задачи. Ис­пользуя уравнения для у и у, получаем следующее.

галлонов,

10x1000

= 5000 галлонов.

>' =

Так как у > у, значит, существует единственное решение для у* и R. Выражение для 5 записывается в следующем виде:

Используя в уравнениях (1) и (2) выражение для 5, получаем следующее.