 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод наименьших квадратов. Если функция регрессии линейна, то говорят, о линейной регрессии
|
|
Если функция регрессии линейна, то говорят, о линейной регрессии.
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
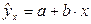 или
или 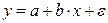 . (2.2)
. (2.2)
Уравнение вида 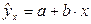 позволяет по заданным значениям фактора
позволяет по заданным значениям фактора  иметь теоретические знания результативного признака подстановкой в него фактических значений фактора
иметь теоретические знания результативного признака подстановкой в него фактических значений фактора 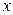 .
.
Построение линейной регрессии сводится к оценке ее параметров – 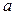 и
и 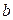 . Оценки параметров линейной регрессии могут быть найдены разными методами.
. Оценки параметров линейной регрессии могут быть найдены разными методами.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
Метод наименьших квадратов позволяет получить такие оценки параметров 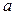 и
и 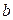 , при которых сумма квадратов отклонений фактических значений результативного признака
, при которых сумма квадратов отклонений фактических значений результативного признака 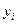 от расчетных
от расчетных 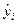
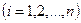 минимальна:
минимальна:
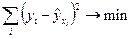 (2.3)
(2.3)
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:
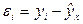 ,
,
следовательно,
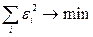 .
.
Для того чтобы найти минимум функции (2.3), надо вычислить частные производные по каждому из параметров 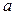 и
и 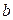 и приравнять их к нулю.
и приравнять их к нулю.
Обозначим 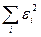 через
через 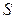 , тогда:
, тогда:
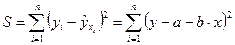

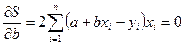 (2.4)
(2.4)
Преобразуя формулу (2.4), получим следующую систему нормальных уравнений для оценки параметров 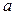 и
и 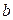 :
:
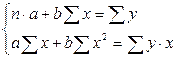 (2.5)
(2.5)
Теперь, разделив обе части уравнений (2.5) на 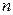 , получим систему нормальных уравнений в виде:
, получим систему нормальных уравнений в виде:
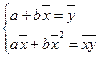 , (2.6)
, (2.6)
где соответствующие средние определяются по формулам:
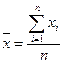 , (2.7)
, (2.7)
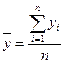 , (2.8)
, (2.8)
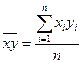 , (2.9)
, (2.9)
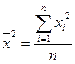 . (2.10)
. (2.10)
Подставляя значение
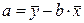 (2.11)
(2.11)
из первого уравнения системы (2.6) в уравнение регрессии 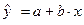 , получим
, получим

или
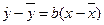 . (2.12)
. (2.12)
Решая систему нормальных уравнений (2.5) либо методом последовательного исключения переменных, либо по формулам Крамера, найдем искомые оценки параметров 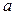 и
и 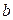 .
.
Поскольку ковариация 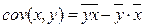 , а дисперсия признака Х
, а дисперсия признака Х 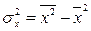 , получим следующую формулу расчета оценки параметра
, получим следующую формулу расчета оценки параметра 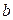 :
:
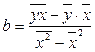 =
= 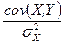 (2.13)
(2.13)
Параметр 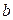 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если функция издержек (У, тыс. руб.) выражается как
называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если функция издержек (У, тыс. руб.) выражается как 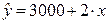 , (
, (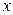 – количество единиц продукции), то, следовательно, с увеличением объема продукции
– количество единиц продукции), то, следовательно, с увеличением объема продукции 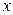 на одну единицу издержки производства возрастают в среднем на 2 тыс. руб., т.е. дополнительный прирост продукции на одну единицу потребует увеличения затрат в среднем на 2 тыс. руб.
на одну единицу издержки производства возрастают в среднем на 2 тыс. руб., т.е. дополнительный прирост продукции на одну единицу потребует увеличения затрат в среднем на 2 тыс. руб.
Знак при коэффициенте регрессии 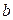 показывает направление связи: при
показывает направление связи: при 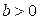 – связь прямая, а при
– связь прямая, а при 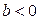 – связь обратная.
– связь обратная.
Параметр 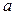 может не иметь экономического содержания.
может не иметь экономического содержания.
Пример 1.
По группе предприятий выпускающих один и тот же вид продукции, рассматривается функция издержек 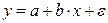 . Необходимая для расчета оценок параметров
. Необходимая для расчета оценок параметров 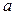 и
и 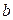 информация представлена в таблице.
информация представлена в таблице.
| Расчетная таблица | ||||||
| Номер предприятия | Выпуск продукции, тыс. ед. 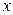
| Затраты на производство, млн. руб. 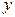
| 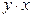
| 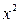
| 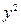
| 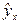
|
| 31,1 | ||||||
| 67,9 | ||||||
| 141,6 | ||||||
| 104,7 | ||||||
| 178,4 | ||||||
| 104,7 | ||||||
| 141,6 | ||||||
| Итого |
Система нормальных уравнений будет иметь вид:
 .
.
Решив ее, получим:
 .
.
Запишем уравнение регрессии:
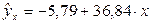
Подставив в уравнение значения 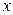 , найдем теоретические значения
, найдем теоретические значения 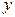 (см. последнюю графу таблицы). В данном случае величина параметра
(см. последнюю графу таблицы). В данном случае величина параметра 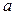 не имеет экономического смысла.
не имеет экономического смысла.
В рассматриваемом примере имеем:
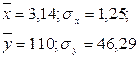
Дата публикования: 2014-11-18; Прочитано: 368 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
