Примеры игр

Рассмотрим несколько примеров формализации игровых или конфликтных ситуаций в виде игр.

Пример 1. Игроки A и B выбирают одну из двух сторон монеты и одновременно показывают друг другу. Если выбранные стороны монет совпали, т.е. обе монеты показываются гербом или решкой, то игрок A выигрывает монету игрока B. Впротивном случае игрок A проигрывает свою монету игроку B. Матрица игры может быть записана следующим образом:

Стратегии игроков	Игрок B
Решка	Герб
Игрок A	Решка		-1
Герб	-1

В этой игре первые стратегии обоих игроков состоят в выборе и предъявлении решки, а вторые стратегии - в выборе и предъявлении герба. Если оба игрока выбрали одинаковые стратегии, то выигрывает первый игрок, если игроки выбрали разные стратегии, то выигрывает второй игрок.

Пример 2. Формализация конфликтной ситуации между двумя фирмами в виде матричной игры.

Пусть на некотором рынке программного обеспечения действуют две сильные фирмы A и B, которые ведут разработку разнообразных программных продуктов параллельно. Разрабатываемые программные продукты могут получаться хорошего качества (Х) и не очень удачными (Н). Пусть в каждую свою разработку первоначально фирмы вкладывают по a единиц денежных средств. Предположим для простоты также, что вопрос пустить в продажу программный продукт или вложить в него дополнительные средства в размере b единиц денежных средств всегда первой решает фирма A. Если фирма A пускает в продажу свой программный продукт, то фирма B также это делает немедленно. При этом та фирма, которая имеет лучшее программное обеспечение, получает от продажи 2 a единиц денежных средств, а вторая фирма не получает ничего. Если же программное обеспечение одного качества (у обеих фирм хорошее или неудачное), то каждая из фирм покрывает свои расходы, получая по a единиц денежных средств за счет продажи своей продукции. Если фирма A не пускает в продажу свое программное обеспечение, а вкладывает в него дополнительные средства, то у фирмы B имеется в распоряжении две альтернативы:

- либо она отказывается от дальнейшей разработки и несет убытки в размере a единиц денежных средств, а фирма A после доработки своего программного обеспечения и продажи получает (2 a + b) единиц денежных средств;

- либо фирма B вкладывает дополнительные средства в размере b единиц и пускает после этого товар в продажу, после чего и фирма A также вынуждена пустить свою разработку в продажу. Если у обеих фирм программные продукты одного качества, то фирмы окупают свои затраты на разработку, получая от продажи по (a + b) денежных единиц. Если же программные продукты разного качества, то фирма с лучшим программным обеспечением получает 2(a + b) единиц денежных средств, а вторая фирма не получает ничего. Все действия фирм можно выразить табл. 1, где фирма A является первым игроком в матричной игре, а фирма B – вторым.

Легко видеть, что фирма A имеет 4 различные стратегические возможности. Первая из них – пустить в продажу, если у нее имеется хорошее программное обеспечение, и пустить в продажу не очень удачное программное обеспечение. Сокращенно это записывается как "продажа - продажа". Другие стратегические возможности фирмы A: "продажа - дополнительные средства", "дополнительные средства - продажа", "дополнительные средства - дополнительные средства". Аналогично и фирма B имеет 4 стратегии, которые подробно описаны в табл. 1.

Рассмотрим действия фирм, когда фирма A выбрала свою первую стратегию "продажа - продажа", а фирма B - свою первую стратегию "продажа, если продает фирма A ¼ – продажа, если продает фирма A ¼". В случае, если обеими фирмами создано хорошее программное обеспечение (Х, Х), обе фирмы компенсируют свои расходы на разработку за счет продажи программных продуктов. Тоже происходит и в случае не очень удачных программных продуктов (Н, Н). В случае если фирма A имеет лучший программный продукт, чем фирма B (Х, Н), то она получает от продажи 2 a единиц денежных средств, а фирма B несет убытки в размере "- a " единиц. В случае, если фирма B имеет лучший программный продукт (Н, Х), то она получает от продажи 2 a единиц денежных средств, а фирма A несет убытки в размере "- a " единиц.

Таблица 1

Хорошее ПО		Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.
Неудачное ПО	Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.
Продажа	Продажа
Продажа	Дополн. средства	3 a/ 4	2 a/ 4	(a - b)/4	-b/ 4
Дополн. средства	Продажа	a/ 4	(a + b)/4		b/ 4
Дополн. средства	Дополн. средства	a	(3 a + b)/4	(a - b)/4

Будем считать, что вероятность появления любой из четырех описанных ситуаций равна 0,25, тогда средний выигрыш фирм при многократном повторении ситуации будет равен нулю:

a ₁₁= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25((-a + a) + (-a + a) + (-a + 2 a) + (-a + 0)) = 0,

где З_ХХ, З_НН, З_ХН, З_НХ - соответственно затраты фирмы A при создании программных продуктов качества (Х, Х), (Н, Н), (Х, Н), (Н, Х);

П_ХХ, П_НН, П_ХН, П_НХ - соответственно денежные средства фирмы A от продажи товара при создании программных продуктов качества (Х, Х), (Н, Н), (Х, Н), (Н, Х).

При расчете элементов a ₁₂, a ₁₃, a ₁₄ аналогично получаем, что a ₁₁ = a ₁₂ = a ₁₃ = = a ₁₄ = 0. Рассмотрим расчет остальных элементов таблицы:

a ₂₁= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25((-a + a) + (- (a + b) + (2 a + b)) + (-a + 2 a) + (- (a + b) + (2 a + b)) = 0,75 a;

a ₂₂= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25((-a +a) + (- (a + b) + (a + b)) + (-a + 2 a) + (- (a + b) + (2 a + b)) = 0,5 a;

a ₂₃= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25((-a +a) + (- (a + b) + (2 a + b)) + (-a + 2 a) + (- (a + b) + 0) = 0,25(a - b);

a ₂₄= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25((-a +a) + (- (a + b) + (a + b)) + (-a + 2 a) + (- (a + b) + 0) = - 0,25 b;

a ₃₁= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25(- (a + b) + (2 a + b)) + (-a+ a) + (- (a + b) + (2 a + b)) + (-a + 0) = 0,25 a;

a ₃₂= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25(- (a + b) + (2 a + b)) + (-a+ a) + (- (a + b) + 2(a + b)) + (-a + 0) =

= 0,25(a + b);

a ₃₃= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =
= 0,25(- (a + b) + (a + b)) + (-a+ a) + (- (a + b) + (2 a + b)) + (-a + 0) = 0;

a ₃₄= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =

= 0,25(- (a + b) + (a + b)) + (-a+ a) + (- (a + b) + 2(a + b)) + (-a + 0) = 0,25 b;

a ₄₁= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =

= 0,25(- (a + b) + (2 a + b)) + (- (a + b) + (2 a + b)) + (- (a + b) + (2 a + b)) +

+ (- (a + b) + (2 a + b)) = a;

a ₄₂= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =

= 0,25(- (a + b) + (2 a + b)) + (- (a + b) + (a + b)) + (- (a + b) + 2(a + b)) +

+ (- (a + b) + (2 a + b)) = 0,25(3 a + b);

a ₄₃= 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =

= 0,25(- (a + b) + (a + b)) + (- (a + b) + (2 a + b)) + (- (a + b) + (2 a + b)) +

+ (- (a + b) + 0) = 0,25(a - b);

a ₄₄ = 0,25((-З_ХХ + П_ХХ) + (-З_НН + П_НН) + (-З_ХН + П_ХН) + (-З_НХ + П_НХ) =

= 0,25(- (a + b) + (a + b)) + (- (a + b) + (a + b)) + (- (a + b) + 2(a + b)) +

+ (- (a + b) + 0) = 0.

Для первого игрока матрица игры является матрицей выигрышей, поэтому анализ первой и третьей стратегий первого игрока показывает, что третья стратегия лучше первой стратегии.

Действительно, сравнивая элементы первой и третьей строк матрицы в соответствующих столбцах, имеем:

0 < a /4; 0 < (a + b)/4; 0 = 0; 0 < b /4.

Таким образом, только при третьей стратегии второго игрока первая и третья стратегии первого игрока равноценны. Во всех остальных случаях первая стратегия уступает третьей, поскольку в отличие от третьей стратегии она не приносит выигрышей первому игроку, т.е. применять первую стратегию первому игроку невыгодно.

Аналогично, четвертая стратегия первого игрока превосходит его вторую стратегию. Следовательно, и вторую стратегию первому игроку применять нет смысла.

Таким образом, число применяемых стратегий первого игрока уменьшается до двух, поэтому исходную матричную игру размерами 4 × 4 можно преобразовать к игре размерами 2 × 4 (табл. 2):

Таблица 2

Хорошее ПО		Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.
Неудачное ПО	Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и отказ от дальнейших разработок, если фирма A вкладывает дополнитель-ные средства.	Продажа, если продает фирма A, и вложение дополнитель-ных средств, если фирма A вкладывает дополнитель-ные средства.
Дополн. средства	Продажа	a/ 4	(a + b)/4		b/ 4
Дополн. средства	Дополн. средства	a	(3 a + b)/4	(a - b)/4

Для второго игрока матрица игры является матрицей проигрышей, поэтому нетрудно видеть, что первая стратегия второго игрока хуже третьей стратегии, а вторая стратегия - четвертой, поскольку элементы соответственно третьего и четвертого столбцов матрицы меньше соответствующих элементов первого и второго столбцов, поэтому применять первую и вторую стратегию второму игроку нет смысла. Следовательно, решение рассматриваемой игры может быть сведено к решению матричной игры 2 ´ 2:

	b/ 4
(a - b)/4

Пример 3. Игра Бореля. Игра Бореля предложена выдающимся французским математиком в 1921 году. В этой игре два игрока A, B выбирают по три неотрицательных числа, сумма которых равна единице, а именно:

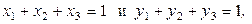
и располагают их в определенном порядке. Игрок A или B выигрывает, если два выбранных ими числа больше соответствующих чисел противника.

Два обобщения игры Бореля

При первом обобщении игроки выбирают по n неотрицательных чисел, удовлетворяющих условиям

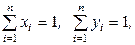(1)

и располагают их в определенном порядке, выигрывает игрок, у которого большее число чисел превосходит числа другого игрока.

При втором обобщении также выбираются по n неотрицательных чисел, удовлетворяющих условиям (1), но при этом выигрывает игрок, у которого больше сумма, определяемая выражениями:

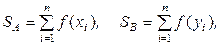
где f - заданная функция.

Игра Бореля может стать игрой на разорение.

Играми на разорение называются многошаговые игры, в которых каждый игрок, начиная игру, имеет ограниченные ресурсы и с каждым шагом или партией ресурсы проигравшего игрока уменьшаются, например, на единицу, на цену игры или на значение, которое вычисляется каким-либо иным способом.

Игра на разорение может быть сформулирована как игра на выигрыш, если считать, что игроки начинают игру с нулевыми ресурсами, а затем на каждом шаге ресурсы выигравшего игрока увеличиваются на единицу или на цену сыгранной партии, или на значение, которое вычисляется каким-либо иным способом.

Пример 4. Игры Блотто. Игра Бореля нашла свое развитие в так называемых играх полковника Блотто - нарицательное имя участника многих иллюстративных игр, имеющих приложения в военной сфере. Рассмотрим пример одной из таких игр.

Два игрока A и B ведут борьбу на N независимых театрах взаимодействия (рынках сбыта, зонах военного конфликта и т.д.), обозначенных числами 1, 2, …, N. Они должны распределить свои силы (ресурсы), соответственно F и G единиц по театрам взаимодействия, не зная схемы распределения противодействующего игрока. Платеж (то есть численная мера выигрыша игрока A или убытки игрока B) на i- ом театре выражается функцией P_i (x, y), зависящей от i- го театра и соотношения ресурсов x и y,вложенных игроками в этот театр взаимодействия. Платеж игры в целом равен сумме платежей на отдельных театрах. Пусть борьба идет на двух театрах, и у A имеется 4 единицы средств, а у его противника - 3, которые нужно распределить между театрами. Платеж определен следующим образом. Игрок получает сумму своих затрат и затрат противника на театре, если он по вложениям превосходит противника,и получает свои затраты, если вложения равны или противник не вкладывал средств в этот театр действий. Если вложения игрока меньше, чем у его противника, то он не получает ничего. Общий платеж равен сумме платежей на обоих театрах действий. Результаты взаимодействия игроков приведены в табл. 3.

Таблица 3

Стратегии	(3, 0)	(0, 3)	(2, 1)	(1, 2)
(4, 0)	(7, 0)	(4, 3)	(6, 1)	(5, 2)
(0, 4)	(4, 3)	(7, 0)	(5, 2)	(6, 1)
(3, 1)	(4, 3)	(3, 4)	(6, 1)	(4, 3)
(1, 3)	(3, 4)	(4, 3)	(4, 3)	(6, 1)
(2, 2)	(2, 5)	(2, 5)	(5, 2)	(5, 2)

За каждой клеточкой матрицы скрывается или окончание игры, как в случае одновременного применения первых или вторых стратегий обоими игроками, или продолжение игры с теми же (например, после применения стратегий (1. 2) или (2, 1)) либо другими ресурсами (например, после применения первым игроком первой стратегии, а вторым - четвертой). В последнем случае будет разыгрываться игра, приведенная в табл. 4.

Таблица 4

Стратегии	(2, 0)	(0, 2)	(1, 1)
(5, 0)	(7, 0)	(5, 2)	(6, 1)
(0, 5)	(5, 2)	(7, 0)	(6, 1)
(4, 1)	(7, 0)	(4, 3)	(6, 1)
(1, 4)	(4, 3)	(7, 0)	(6, 1)
(3, 2)	(7, 0)	(5, 2)	(7, 0)
(2, 3)	(5, 2)	(7, 0)	(7, 0)

В игре Блотто выигрывает тот, кто истощит ресурсы противника.