Лабораторная работа № 6. Цель лабораторных занятий

"ФОРМАЛИЗАЦИЯ кОНФЛИКТНЫХ СИТУАЦИЙ С ПОМОЩЬЮ

ТЕоРиИ ИГР"

Цель лабораторных занятий

Приобретение и закрепление знаний, и получение практических навыков работы при формализации конфликтных ситуаций с помощью теории игр.

Краткие сведения из теории

Основные понятия и определения теории игр

Теория игр - раздел математики, изучающий методы принятия решений в конфликтных ситуациях.

Игра - математическая модель конфликтной ситуации, в которой определены участники конфликта (игроки), их возможные действия (стратегии), получаемая ими информация, условия окончания игры и правила изменения заинтересованности каждого игрока.

Партия игры - случай разыгрывания игры некоторым конкретным образом от начала до конца.

В настоящее время нет общепризнанной классификации игр, но можно отметить несколько основных направлений, используемых для классификации игр: число игроков и стратегий, характер взаимоотношения игроков, число ходов, характер и вид функций выигрышей и т.д.

В зависимости от числа игроков различают игры двух и n игроков. Наибольшее распространение получили игры двух игроков. Они наиболее исследованы и широко применяются на практике. Игры n игроков менее исследованы и применяются реже, поскольку их решение существенно сложнее, чем игр двух игроков, причем трудности решения игр возрастают с ростом числа игроков.

По числу стратегий все игры можно разделить на конечные и бесконечные. Игра называется конечной, если каждый из игроков имеет конечное число стратегий. В противном случае игра называется бесконечной.

По характеру взаимоотношения игроков различают коалиционные, кооперативные и бескоалиционные игры. Если в процессе игры игроки могут вступать в соглашения и образовывать коалиции, то такая игра называется коалиционной. Если коалиции определены заранее, то игры называются кооперативными. Если в процессе игры игроки не могут вступать в соглашения и образовывать коалиции, то такие игры называются бескоалиционными.

В зависимости от числа ходов игры делятся на одношаговые и многошаговые. Игра называется одношаговой, если каждый из игроков делает по одному шагу. Если хотя бы один из игроков делает более одного шага, то игра называется многошаговой.

По характеру выигрышей игры делят на игры с нулевой суммой и игры с ненулевой суммой. Если сумма выигрышей всех игроков в каждой партии равна нулю, то игра называется игрой с нулевой суммой. В такой игре сумма общего капитала всех игроков остается неизменной и в зависимости от исхода партии он перераспределяется между игроками. Таким образом, в играх с нулевой суммой выигрыши одних игроков оборачиваются потерями других игроков. В случае игры двух игроков их цели становятся диаметрально противоположными, поскольку выигрыш одного игрока равен проигрышу другого игрока. Такие игры двух игроков с нулевой суммой называют антагонистическими. Многие политические, военные и экономические ситуации математически можно описывать как игры с нулевой суммой.

В играх с ненулевой суммой общий капитал всех игроков меняется в процессе игры, поэтому все игроки могут быть в выигрыше. Примером таких игр могут быть игры, моделирующие взаимовыгодные торговые отношения между странами.

По виду функций выигрышей различают следующие виды игр: матричные, биматричные, выпуклые, непрерывные и т.д.

Матричная игра - это конечная одношаговая антагонистическая игра двух игроков, в которой выигрыши первого игрока задаются с помощью матрицы размерностью n ´ m, где n - число строк и стратегий первого игрока; m - число столбцов и стратегий второго игрока. Каждой паре стратегий (i, j) соответственно первого и второго игроков поставлено в соответствие число a_ij, которое является выигрышем первого игрока за счет второго, если a_ij > 0. Если a_ij < 0, то при данной паре стратегий выигрывает второй игрок. Указанная матрица называется матрицей игры или платежной матрицей. Матричную игру с матрицей n × m часто называют игрой n × m.

Стратегии i и j (i Î {1, 2, ¼, n }, j Î {1, 2, ¼, m }) соответственно первого и второго игроков часто называют чистыми стратегиями.

Решение матричной игры состоит в определении наилучшей или оптимальной стратегии для каждого из игроков. Поскольку выбор наилучшей стратегии каждым из игроков производится при отсутствии информации о действиях другого игрока, то можно дать следующее определение наилучшей или оптимальной стратегии, одного из основных понятий теории игр.

Стратегия игрока называется оптимальной, если ее применение обеспечивает игроку наибольший гарантированный выигрыш при любых возможных стратегиях другого игрока.

Исходя из этого определения, исследуем матрицу выигрышей A = 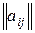первого игрока

.

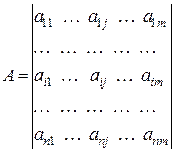Если первый игрок выберет стратегию i (i Î {1, 2, ¼, n }), то второй игрок будет стремиться к тому, чтобы выбором своей стратегии j (j Î {1, 2, ¼, m }) выигрыш первого игрока, а, следовательно, и свой проигрыш свести к минимуму:

, .

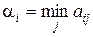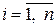Из минимальных элементов a _i каждой строки формируется дополнительный столбец. Первый игрок будет стремиться найти такую стратегию i, при которой величина 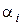достигает максимального значения, поэтому он из этого столбца выделяет максимальный элемент:

.

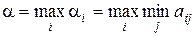Число a называют нижней чистой ценой игры. Оно показывает, какой минимальный выигрыш может гарантировать себе первый игрок, придерживаясь своей максиминной стратегии.

Оптимальное поведение второго игрока состоит в том, что он с помощью своих стратегий должен максимально уменьшить выигрыш первого игрока, т.е. для каждой своей стратегии j он должен определить свой максимальный возможный проигрыш 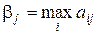, сформировать из этих проигрышей дополнительную строку, а затем с помощью этой строки выбрать стратегию, при которой величина 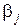минимальна:

.

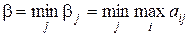Число b называется верхней чистой ценой игры. Оно показывает, что второй игрок за счет применения своей минимаксной стратегии может не допустить выигрыша первого игрока больше, чем b.

Таким образом, за счет оптимального применения своих чистых стратегий первый игрок может гарантировать себе выигрыш не меньше, чем a, а второй игрок – что его проигрыш не будет больше, чем b.

Если в матричной игре A нижняя и верхняя чистые цены игры совпадают, то говорят, что матричная игра A имеет седловую точку в чистых стратегиях и чистую цену игры .

Седловой точкой в матричной игре A называется пара (i ₀, j ₀) чистых стратегий соответственно первого и второго игроков, при которых достигается равенство между верхней и нижней чистыми ценами игры .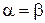

Элемент 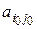матрицы A, стоящий на пересечении строки 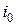и столбца 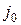называют седловой точкой матричной игры, а число – чистой ценой игры.

Понятие седловой точки несет определенный смысл. Рассмотрим его. Если в матричной игре A имеется седловая точка и один из игроков придерживается стратегии, соответствующей седловой точке, то у другого игрока нет лучшей стратегии, чем также придерживаться седловой точки. Действительно, если седловой точки придерживается первый игрок, а второй игрок хочет выбрать стратегию , то поскольку по определению b элемент 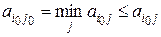, т.е. является минимальным в дополнительной строке, то второй игрок не может уменьшить свой проигрыш, но может его увеличить. 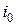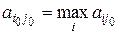Если седловой точки придерживается второй игрок, а первый хочет изменить стратегию на , то поскольку по определению a элемент и 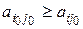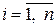, то первый игрок не сможет увеличить свой выигрыш за счет замены стратегии 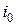на любую другую, но может уменьшить свой выигрыш, так как элемент 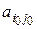является максимальным элементом 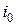дополнительного столбца. Таким образом, имеем

,

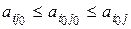где i, j – соответственно произвольные чистые стратегии первого и второго игроков; 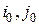– чистые стратегии первого и второго игроков, соответствующие седловой точке; – произвольный элемент столбца 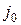матрицы A; 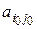– седловой элемент матричной игры; 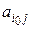– произвольный элемент строки 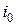матрицы A.

Седловой элемент 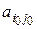является минимальным элементом строки 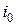и максимальным элементом столбца 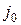. Это свойство седлового элемента позволяет предложить простой алгоритм для определения седловых точек: последовательно в каждом столбце определяют максимальный элемент и проверяют, является ли он минимальным элементом в своей строке. Если проверяемый элемент удовлетворяет этому условию, то он и является седловым элементом, а соответствующая ему пара чистых стратегий образует седловую точку. Естественно, что поиск седловых точек можно осуществить и отыскивая в каждой строке минимальный элемент, а затем проверяя, является ли он максимальным в столбце.

Решением матричной игры A в чистых стратегиях называется пара чистых стратегий , образующих седловую точку, и седловой элемент .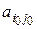

Стратегии 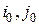, соответственно первого и второго игроков в матричной игре A, называют оптимальными чистыми стратегиями.

Если в матричной игре нет седловой точки в чистых стратегиях, то в этом случае 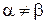и и получить решение матричной игры в чистых стратегиях не удается. Можно только определить, что цена игры v находится между a и b. Для поиска более точного решения матричной игры в подобных случаях необходимо применять методы, основанные не на чистых, а на смешанных стратегиях обоих игроков.

Биматричная игра - это конечная одношаговая бескоалиционная неантагонистическая игра двух игроков, в которой выигрыши каждого игрока задаются с помощью отдельной матрицы размерностью n ´ m, где n - число строк и стратегий первого игрока; m - число столбцов и стратегий второго игрока.

Непрерывная игра - это бесконечная игра с непрерывными функциями выигрышей каждого из игроков, стратегиями которых обычно являются числа из определенного интервала. Если функции выигрышей в игре являются не только непрерывными, но и выпуклыми, то такая игра называется выпуклой.