Прямые методы решения СЛАУ. Метод прогонки

Одной из самых распространённых задач вычислительной математики является решение систем линейных алгебраических уравнений и ряда связанных с ним вопросов, таких как вычисление определителей, обращение матриц, отыскание их собственных значений. Этот круг вопросов называется задачами линейной алгебры. Система из n - линейных алгебраических уравнений с n - неизвестными имеет вид: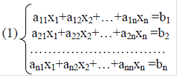

где аij, bi-известные величины, Хi- неизвестные.

Система (1) в сокращённом виде: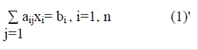

Система (1) в матричном виде:

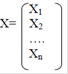
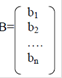
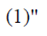
Известно, что система (1) имеет единственное решение, если определитель матрицы:

Δ=det A не равен нулю.

В противном случае система (1) не имеет решения, либо имеет бесконечное множество решений. Будем считать, что Δ = detA не равен нулю.

Для решения системы (1) имеются две группы методов: прямые и итерационные методы.

Прямыми называют такие методы, которые используют конечные соотношения (формулы) для выполнения заранее известного числа операций. При этом, если исходные данные точны, то результат будет точным, поэтому прямые методы называют точными методами. Но исходные данные обычно не точны и при решении задачи прямыми методами происходит накопление погрешностей. Чем больше число уравнений, тем больше погрешностей, поэтому прямые методы используют, если n<200.

К прямым методам относятся, формулы Крамера, метод Гауса, метод Жордана и метод прогонки.

Итерационные методы позволяют построить последовательность, сходящуюся к точному решению, и позволяют решить задачу с любой заранее заданной точностью. При применении итерационных методов накопления погрешностей не происходит, однако _______они требуют выполнения гораздо большего числа арифметических операций.

Метод прогонки. При решении практических задач получаются системы, матрицы которых содержат много нулей, то говорят, что система имеет слабо заполненную матрицу. Эти нули обычно располагаются массивами в определённых местах матрицы.

Если применить к таким системам метод Гаусса, то нулевые элементы будутвовлечены в вычислительныйпроцесс, что не желательно. Поэтому, созданы специальные методы, позволяющие обходить нулевые элементы. Одним изтаких методов является метод прогонки, он применяется к системам с ленточной матрицей.

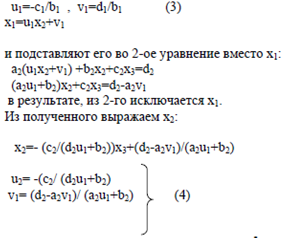x2= u2х3+ v1, полученное выражение х2 в 3 -е уравнение, чтобы исключить х2 и т.д., то на i-ом шаге исключения получим формулу:

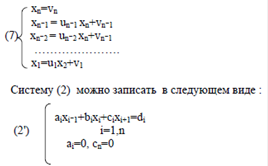
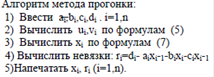
Прямые методы. Формула Крамера

Ах+В

Хi=ΔΔi, i=1, n

Δ- определитель матрицы. Δi - определитель матрицы, получаемой заменой i--го столбца матрицы столбцом из свободных членов:

2х+3y=7 -x+4y=3 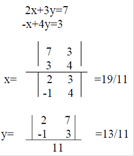Формула Крамера при небольших n требует приблизительно nn!- операций.

Наиболее распространённым среди прямых методов является метод исключения Гаусcа. Метод приводит к значительно меньшему объёму вычислений, чем формула Крамера. Метод Гаусcа состоит из прямого и обратного хода. Прямой ход - это приведение матрицы системы к верхнему треугольному виду, иначе говоря, система преобразуется т.о., чтобы исключить х1 из всех уравнений кроме 1-го, х2- из всех кроме 1-го и 2-го. Для этого делим 1-ое уравнение на а11, умножаем на аi1 и вычитаем из i-го уравнения системы.i=2,3…n.

В результате, из всех кроме 1-го уравнения исключается х1, затем с помощью 2-го х2 и т.д.

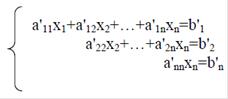
- это треугольная матрица. Теперь обратный ход, непосредственного вычисления неизвестных.

Из n-го уравнения находим хn: 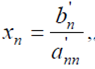полученное значение в xn подставляем в (n-1), откуда находим x(n-2) и т.д. Метод Гаусса требует выполнения 2/3n^3 - операций.