Математическое ожидание

Как уже говорилось выше, моменты более высоких порядков в метрологии обычно не используются.

Первый начальный момент – математическое ожидание – представляет собой оценку истинного значения случайной величины. Как уже говорилось выше, на практике при измерениях обычно имеют дело со случайными дискретными величинами – результатами измерений.

Математическое ожидание случайной дискретной величины представляет собой сумму произведений всех ее возможных значений на вероятности их появления.

Предположим, что случайная величина может принимать только значения х₁, х₂,…х_n, вероятности появления которых соответственно равны p₁, p₂,…p_n. Тогда математическое ожидание случайной дискретной величины Х определится следующим образом:

M(X) = 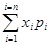(5.4).

Необходимо особо подчеркнуть, что математическое ожидание случайной величины есть величина не случайная, а постоянная и вполне определенная. Пример. Найти математическое ожидание случайной величины Х, зная закон ее распределения:

Х
р	0,1	0,6	0,3

Искомое математическое ожидание М(Х) = 3·0,1+5·0,6+2·0,3 =3,9.

Математическое ожидание обладает следующими четырьмя свойствами.

Свойство 1. Математическое ожидание постоянной величины С равно самой величине, т.е.

М(Х)=С.

Доказательство. Будем рассматривать постоянную С как дискретную случайную величину, которая имеет только одно возможное значение С и принимает его с вероятностью р=1. Тогда

М(С)= С·1=С (5.5).

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания, т.е.

М(СХ)=СМ(Х) (5.6).

Доказательство. Предположим, что случайная величина Х задана следующим законом распределения вероятностей:

Х	х1	х2	хn
р	Р1	Р2	pn

Будем рассматривать каждую величину х₁, х₂,… х_n как произведение 1·x_i. Тогда математическое ожидание

М(СХ)= C х₁·р₁ +C х₂·р₂ +…+C х_nр_n =С(х₁·р₁+ х₂·р₂+…+х_nр_n) = СМ(Х).

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M(XY)=M(X)·M(Y).

Доказательство. Зададим независимые случайные величины своими законами распределения вероятностей:

Х	х1	х2	Y	y1	y2
р	р1	р2	q	q1	q2

Выразим все значения, которые может принимать случайная величина XY, перемножив все возможные значения Х на каждое значение Y: (х₁ y₁), (х₂ y₁), (х₁ y₂), (х₂ y₂). Учитывая, что если вероятность появления х₁ равна р₁, а вероятность появления y₁ равна q₁, то вероятность появления (х₁ y₁), равна (р₁ q₁) и т.д ., получим:

М(Х Y)= (х₁ y₁) (р₁ q₁)+ (х₂ y₁) (р₂ q₁)+ (х₁ y₂) (р₁ q₂)+ (х₂ y₂) (р₂ q₂)=

=y₁ q₁(х₁ р₁+х₂ р₂) + y₂ q₂(x₁ p₁+ x₂ p₂)= (x₁ p₁ + x₂ p₂₎(y₁ q₁+ y₂ q₂)=

= (М(Х)·М(Y).

Т.е. М(Х Y)= М(Х)·М(Y) (5.7).

Следствием этого свойства является то, что математическое ожидание произведения нескольких независимых случайных величин равно произведению их математических ожиданий:

М(Х Y·Z)= М(Х) М(Y) М(Z) (5.8).

Свойство 4. Математическое ожидание суммы двух независимых случайных величин равно сумме их математических ожиданий:

М(Х+Y)= М(Х)+М(Y) (5.9).

Доказательство. Предположим, что случайные величины Х и Y заданы своими законами распределения вероятностей:

Х	х1	х2	Y	y1	y2
р	р1	р2	q	q1	q2

Составив все возможные значения величины Х+ Y, получим:

(х₁+ y₁), (х₁+ y₂), (х₂+ y₁), (х₂+ y₂).

Математическое ожидание величины Х+ Y равно сумме произведений всех ее возможных значений на соответствующие вероятности:

М(Х+Y)= (х₁+ y₁) р₁ q₁+ (х₁+ y₂) р₁ q₂+ (х₂+ y₁) р₂ q₁+ (х₂+ y₂) р₂ q₂.

После обычных преобразований получим:

М(Х+Y)= х₁(р₁ q₁+ р₁ q₂)+ х₂(р₂ q₁+ р₂ q₂)+ y₁(р₁ q₁+ р₂ q₁)+ y₂(р₁ q₂+ р₂ q₂).

Докажем, что:

(р₁ q₁+ р₁ q₂₎= р₁, (р₂ q₁+ р₂ q₂₎₌ р₂, (р₁ q₁+ р₂ q₁)= q₁, (р₁ q₂+ р₂ q₂)= q₂.

Событие, состоящее в том, что Х примет значение х₁ (вероятность этого события равна р₁), влечет за собой событие, которое состоит в том, что Х+Y примет значение х₁+ y₁ или х₁+ y₂ (вероятность этого события по теореме сложения равна (р₁ q₁+ р₁ q₂= р₁) и обратно. Аналогично доказывается, что

р₂ q₁₊ р₂ q₂= р₂ и т.д.

Тогда, х₁(р₁ q₁+ р₁ q₂)+ х₂(р₂ q₁+ р₂ q₂)= М(Х), y₁(р₁ q₁+ р₂ q₁)+ y₂(р₁ q₂+

+р₂ q₂)= М(Y).

Таким образом, М(Х+Y)= М(Х)+М(Y).

Следствием этого свойства является то, что математическое ожидание суммы нескольких независимых случайных величин равно сумме их математических ожиданий:

М(Х+Y+Z)= М(Х)+ М(Y)+ М(Z) (5.10).

Вероятностный смысл математического ожидания заключается в том, что при достаточно большом числе независимых испытаний (чем больше, тем точнее), оно приближенно равно среднему арифметическому значению этого ряда чисел.

Пусть проведено n испытаний, в которых величина Х приняла m₁ раз приняла значение х₁, m₂ – х₂, х_k – m_k, причем m₁+ m₂+…+ m_k= n.

Сумма всех значений, которые приняла величина Х в n независимых испытаний, определится следующим образом:

= х₁ m₁+ х₂ m₂+…+ х_k m_k.

Разделив левую и правую часть этого равенства на n, получим:

= = (х₁ m₁+ х₂ m₂+…+ х_k m_k)/ n = х₁( m₁/ n)+ х₂( m_2/ n)+ … +

+ х_k (m_k/ n) (5.11),

где отношения ( m₁/ n), ( m₂/ n), … (m_k/ n) представляют собой относительную частоту w _k (частность) выпадения соответствующих значений х_k.

В соответствии с теоремой Бернулли: Если в каждом из n независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты w от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико, принимаем w _k≈ р.

Таким образом,

х₁( m₁/ n)+ х₂( m_2/ n)+…+ х_k (m_k/ n) = х₁ w ₁+ х₂ w _k+… х_k w _k≈

≈ х₁ р₁ + х₂р₂+…+ х_kр_k=М(Х), т.е. = М(Х) (5.12).

Этот вывод имеет большое практическое значение, т.к. обычно на практике при обработке результатов измерений для оценки истинного значения измеряемой физической величины наиболее часто используют именно среднее арифметическое значение ряда наблюдений, а не математическое ожидание или какой-либо другой параметр.

Математическое ожидание, как и мода Мо(х), и медиана Ме(х) относятся к характеристикам положения функции распределения случайной величины.

Модой называют значение случайной величины, имеющей у дискретной величины наибольшую вероятность, а у непрерывной – наибольшую плотность вероятности. Если кривая распределения имеет один максимум, то мода равна значению случайной величины, соответствующей этому максимуму. Такая кривая называется одномодальной (рис. 5.1). Если кривая распределения имеет два или несколько максимумов, то она, соответственно называется двухмодальной или многомодальной (рис. 5.2).

Медианой случайной величины Х называют такое ее значение, для которого функция распределения равна 0,5 (рис. 5.3).

Рис. 5.1

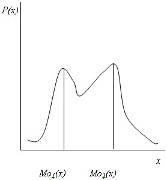
Рис. 5.2

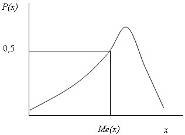
Рис. 5.3

Размещено на Allbest.ru