 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Функция распределения дискретной случайной величины
|
|
Функцией распределения (вероятностей) случайной величины  называется функция
называется функция  , определяющая вероятность того, что случайная величина
, определяющая вероятность того, что случайная величина  в результате испытания примет значение, строго меньшее
в результате испытания примет значение, строго меньшее  , т. е.
, т. е.
 . (23)
. (23)
Функцию  называют интегральным законом распределения случайной величины.
называют интегральным законом распределения случайной величины.
Функция распределения любой дискретной случайной величины есть разрывная кусочно-постоянная функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений.
Рассмотрим основные свойства функции распределения дискретной случайной величины.
1. Значения функции распределения принадлежат отрезку [0,1]:
 .
.
2. Функция распределения есть неубывающая функция на всей числовой оси, т. е.
 , если
, если  .
.
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице, т. е.
 ,
,  .
.
4. Вероятность попадания случайной величины в полуинтервал [  ) равна приращению её функции распределения на этом полуинтервале, т. е.
) равна приращению её функции распределения на этом полуинтервале, т. е.
 .
.
Следствие 1. Если возможные значения случайной величины  принадлежат числовому отрезку [
принадлежат числовому отрезку [  ], то
], то
 при
при 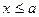 и
и  при
при  .
.
Следствие 2. Для дискретной случайной величины  функция распределения
функция распределения  равна сумме вероятностей тех её значений, которые строго меньше
равна сумме вероятностей тех её значений, которые строго меньше  , т. е.
, т. е.
 .
.
Пример 28. Случайная величина  задана рядом распределения:
задана рядом распределения:
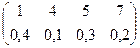 .
.
Найти функцию распределения вероятностей и построить её график.
Решение. Если  , то
, то  (следствие 1).
(следствие 1).
Если  , то
, то  .
.
Действительно, имеется единственное возможное значение случайной величины ( ), которое строго меньше 4, и вероятность этого события
), которое строго меньше 4, и вероятность этого события  по условию равна 0,4.
по условию равна 0,4.
Пусть  . Тогда
. Тогда  .
.
Действительно, если  удовлетворяет неравенству
удовлетворяет неравенству  , то
, то  по определению равно вероятности события
по определению равно вероятности события  , которое может произойти, когда
, которое может произойти, когда  примет значение 1 (вероятность этого события 0,4) или значение 4 (вероятность его равна 0,1).
примет значение 1 (вероятность этого события 0,4) или значение 4 (вероятность его равна 0,1).
Но так как эти события несовместны, то по теореме сложения вероятностей:
 0,5.
0,5.
Если  , то по аналогии
, то по аналогии  , так как три значения случайной величины
, так как три значения случайной величины  (1,4,5) строго меньше её значения 7.
(1,4,5) строго меньше её значения 7.
Наконец, если  , то
, то  (следствие 1).
(следствие 1).
В итоге функция распределения аналитически может быть записана в виде:

Построим её график, откладывая по оси абсцисс значения случайной величины, а по оси ординат – их вероятности (рис. 2).

Рис. 2
Пример 29. Из пяти гвоздик две белые. Составить закон распределения и найти функцию распределения случайной величины, выражающей число белых гвоздик среди двух одновременно взятых.
Решение. Пусть случайная величина  число белых гвоздик среди двух одновременно взятых.
число белых гвоздик среди двух одновременно взятых.
Она может принимать значения: 0,1,2.
Найдем вероятности событий 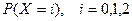 с использованием классической формулы вероятности.
с использованием классической формулы вероятности.
Общее число исходов определяется числом сочетаний из пяти элементов по два, так, как порядок гвоздик не имеет значения, т. е
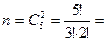 10.
10.
Событию  благоприятствует
благоприятствует 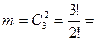 3 исхода.
3 исхода.
Тогда  0,3.
0,3.
Событию 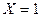 благоприятствует
благоприятствует  6 исходов.
6 исходов.
Отсюда  0,6. Наконец, число исходов, благоприятствующих событию
0,6. Наконец, число исходов, благоприятствующих событию 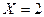 , равно
, равно  1 и
1 и 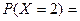 0,1.
0,1.
Ряд распределений случайной величины  имеет вид:
имеет вид:
 .
.
В результате функция распределения аналитически записывается:

Пример 30. Функция распределения случайной величины  имеет вид:
имеет вид:

Найти вероятность того, что:
а) 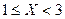 ;
;
б)  .
.
Решение. а). С использованием свойства 4 функции распределения имеем
 0,3.
0,3.
б). События ( ) и (
) и ( ) являются противоположными. Тогда
) являются противоположными. Тогда
 .
.
Но вероятность  по определению равна значению функции распределения в точке 1/3, т. е.
по определению равна значению функции распределения в точке 1/3, т. е.  . Отсюда
. Отсюда
 0,3.
0,3.
Пример 31. В примере 26 найти функцию распределения для случайной величины  .
.
Решение. В результате решения примера 26 был найден ряд распределения случайной величины  :
:
 .
.
Если  , то по следствию 1:
, то по следствию 1:  .
.
Когда  , то
, то  .
.
Пусть  . Тогда в силу следствия 2 функция распределения
. Тогда в силу следствия 2 функция распределения  возрастает на величину
возрастает на величину  :
:  .
.
Для 
 .
.
В полуинтервале  функция
функция  .
.
Наконец при  имеем
имеем  .
.
В итоге случайная величина  имеет следующую функцию распределения:
имеет следующую функцию распределения:
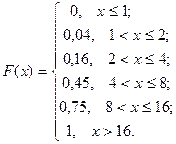
Дата публикования: 2015-11-01; Прочитано: 6983 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
