Законы распределения. Числовые характеристики

Случайная величина называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, конечного числа точек.

Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю .

Вероятность попадания непрерывной случайной величины в интервал () не зависит от того, является ли этот интервал открытым или закрытым, т.е.

.

Плотностью распределения вероятности 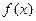непрерывной случайной величины называется производная ее функции распределения .

Плотность вероятности 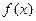называют дифференциальным законом распределения случайной величины .

Основные свойства плотности распределения вероятности:

1. Плотность вероятности является неотрицательной функцией

.

2. Вероятность попадания непрерывной случайной величины в интервал () равна определенному интегралу от ее плотности вероятности в пределах от до

.

3. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице

.

4. Функция распределения непрерывной случайной величины связана с плотностью вероятности формулой

.

Математическим ожиданием непрерывной случайной величины называется несобственный интеграл

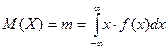, (29)

если он сходится.

Дисперсией непрерывной случайной величины называется несобственный интеграл

, (30)

если он сходится.

Математическое ожидание и дисперсия непрерывной случайной величины обладают теми же свойствами, что и те же характеристики дискретной случайной величины.

Модой непрерывной случайной величины называют точку, в которой плотность вероятности достигает максимума.

Медианой непрерывной случайной величины называют такое ее значение, для которого

.

Квантилем уровня называется такое значение случайной величины, при котором функция распределения принимает значение, равное , т.е.

.

Начальным моментом го порядка случайной величины называется математическое ожидание й степени этой величины

.

Центральным моментом го порядка случайной величины называется математическое ожидание й степени отклонения случайной величины от ее математического ожидания

.

Коэффициентом асимметрии случайной величины называют отношение

,

которое характеризует скошенность распределения.

Эксцессом случайной величины называют число

,

которое характеризует островершинность распределения.

Пример 36. Дана функция распределения вероятности непрерывной случайной величины :

Найти плотность распределения 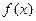и построить графики обеих функций.

Решение. Плотность вероятности равна первой производной функции распределения:

Заметим, что при 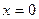производная не существует.

Рис. 3.

Пример 37. Непрерывная случайная величина задана функцией распределения:

Необходимо:

1. Найти плотность вероятности .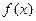

2. Построить графики функций .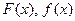

3. Определить вероятности .

4. Вычислить .

Решение. 1. Дифференцируя функцию распределения , находим плотность вероятности:

2. Используя аналитическое задание функций 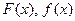, строим их графики (рис. 4).

3. , как вероятность отдельного значения непрерывной случайной величины.

Рис. 4.

Вероятность находится либо по определению функции распределения

либо по свойству 2 плотности распределения

.

Вероятность можно найти либо как приращение функции распределения

,

либо по свойству 2 плотности вероятности

.

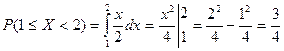4. Математическое ожидание находим по формуле (29)

.

По свойству дисперсии .

Вначале определим

и далее

.

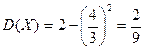Плотность вероятности 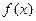максимальна при , отсюда по определению моды 2.

Обозначим 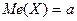и найдем медиану либо из условия , т.е.

,

либо через плотность вероятности

.

Откуда

.

Пример 38. Дана плотность вероятности 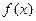случайной величины :

Найти функцию распределения .

Решение. Воспользуемся свойством 4: .

Если , то и, следовательно, .

При .

Наконец, если , то .

В итоге получаем:

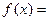
Пример 39. Плотность распределения вероятностей в интервале () равна и 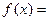0 вне этого интервала. Найти постоянную .

Решение. Плотность вероятности удовлетворяет свойству 3: .

Отсюда

.

В итоге имеем 1.