Повторение испытаний

Пусть производится 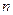испытаний, причём вероятность некоторого события в каждом испытании не зависит от исходов других испытаний, постоянна и равна .

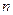Тогда вероятность того, что событие наступит ровно раз в независимых испытаниях, определяется по формуле Бернулли

, . (14)

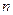Наивероятнейшее число появлений события раз в независимых испытаниях, определяется из двойного неравенства:

, (15)

где .

При больших значениях 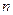и пользоваться формулой (14) для вычислений неудобно. Если вероятность постоянна и мала, число испытаний велико, а число незначительно (), то для вычисления вероятности можно использовать приближенную формулу Пуассона:

, (16)

где функция Пуассона, значения которой приводятся в приложении 3.

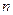Если вероятность удовлетворяет условию: , число испытаний велико, а , то вероятность можно найти по приближенной локальной формуле Муавра-Лапласа:

, (17)

где

- функция Гаусса, значения которой приводятся в приложении 1,

а .

В этих условиях для нахождения вероятности события можно воспользоваться интегральной формулой Муавра-Лапласа:

, (18)

где

- функция Лапласа, значения которой приводятся в приложении 2.

Пример 19. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: две партии из четырёх или три партии из шести (ничьи во внимание не принимаются)?

Решение. Поскольку игроки равносильные, то вероятность выигрыша партии всегда постоянна и равна =0,5. Здесь применима формула Бернулли (14).

Найдем вероятность того, что две партии из четырёх будут выиграны:

.

Далее вычислим вероятность того, что будут выиграны три партии из шести:

.

Поскольку , то вероятнее выиграть две партии из четырёх, чем три из шести.

Пример 20. Завод отправил на базу 10 000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке, составляет 0,002% Найти вероятность того, что из 10 000 изделий:

а) будет повреждено три изделия;

б) будет повреждено, по крайней мере, три изделий;

в) Не будет повреждено 9997 изделий.

Решение.

а). Вероятность того, что изделие будет повреждено при транспортировке, равна =0,0002. Так как мала, а 10 000 – велико, но при этом , то для 3 применима формула Пуассона (16):

0,1805.

Значение функции Пуассона =0,1805 определяем по приложению 3.

б) Вероятность может быть вычислена как сумма большого числа слагаемых

.

Отсюда её проще найти через вероятность противоположного события:

0,3233.

в) Вероятность «неповреждения» изделия при транспортировке равна

0,9998 и требуется найти .

Однако формулу Пуассона применять нельзя, ибо 0,9998 велика.

Но событие «не будет повреждено 9997 изделий из 10 000» равносильно событию «будет повреждено 3 изделия из трёх», вероятность которого найдена в пункте а), т. е. =0,1805.

Пример 21. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.

Решение. Имеем повторение испытаний, когда 400 и 300.Вероятность того, что наудачу выбранная семья имеет холодильник, равна

0,8.

Поскольку велика, а , то формулу Пуассона применять нельзя (она даст большую ошибку). Но выполняется неравенство и поэтому применима локальная формула Муавра-Лапласа (17).

Вначале определяем

-2,5.

Далее по таблице функции Гаусса (приложение 1) находим в силу её четности

0,075.

Наконец, по формуле (17) вычисляем

0,0022.

Пример 22. По результатам проверки налоговыми инспекторами установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. Найти вероятность того, что из 1000 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины:

а) от 480 до 520 предприятий;

б) наивероятнейшее число предприятий.

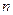Решение. а) Рассматривая задачу как схему повторения испытаний при =0,5, заметим, что =1000 велико, но и можно использовать интегральную формулу Муавра-Лапласа (18).

Вначале определим:

-1,265;

1,265.

По таблице (приложение 2) находим значение функции Лапласа, которая является нечётной:

.

Тогда

0,794.

б) Наивероятнейшее число появления события в схеме независимых испытаний определяется формулой (15).

Отсюда

или

.

Единственное целое число, удовлетворяющее этим неравенствам – это =500. Найдем вероятность этого события по локальной формуле Муавра-Лапласа (17):

0,

,

0,0252.