Условия возникновения циркуляции

1. Время между посылкой двух импульсов возбуждения (Т) должно быть меньше периода рефрактерности R₂ >T.

2. Длина окружности кольца должна быть больше длины волны возбуждения.

Длина циркулирующей волны (при скорости 3 м/с и периоде примерно в 0,3 с) в путях проведения может быть около 1 м, поэтому ее появление анотамически невозможно. Однако в узлах медленного проведения возбуждения, где скорость может быть около 0,01 м/с, а длина волны порядка нескольких мм. Поэтому механизм циркуляции волны возбуждения в сердце возможен (например в области артиовентрикулярного узла и в зонах с замедленным проведением автоволн.

26. АВТОВОЛНОВЫЕ ПРОЦЕССЫ В СЕРДЕЧНОЙ МЫШЦЕ

Мышечная ткань представляет собой возбудимую среду. Возбуждение, сообщаемое сетью нервных волокон, вызывает механохимические процессы. Процессы в возбудимых средах имеют важнейшее значение в физиологии, в частности, в физиологии сердечной мышцы.

В возбудимой среде распространение импульса происходит без затухания за счет энергии клеток. Импульс генерируется каждой точкой среды. Пример однородной возбудимой среды – нервное волокно. Каждая точка возбудимой среды может находиться в одном из трех состояний: покоя, возбуждения, рефрактерности. Если на малый участок волокна, находящегося в состоянии покоя, подать возбуждение, то он перейдет в возбужденное состояние, в котором будет находиться некоторое время t, затем перейдет в рефрактерное состояние, в котором будет пребывать t_R. В период рефрактерности t_R участок не реагирует на возбуждающий сигнал, поэтому данный участок не может возбуждаться с частотой, большей t ^-1_R.

В возбудимых средах реализуются автоволновые процессы. Источники волн могут возникать и в таких средах, в которых ни один из элементов не способен возбуждаться самопроизвольно, то есть не является автоколебательным. Возникновение таких источников обусловлено особыми свойствами среды и волны возбуждения.

При рассмотрении реакций Белоусова – Жеботинского было отмечено существование источников волн двух типов – с ведущими центрами (ЭХО), посылающими концентрические волны, и с ревербераторами – вращаю-щимися спиральными волнами. Возникновение и последующее размно-жение ревербераторов играет важнейшую роль в механизме фибриляции - очень опасной сердечной аритмии. Аритмия означает нарушение синх-ронизации распространения волн в сердечной мышце: вместо синхронных сокращений возникают беспорядочные колыхания, и организм быстро погибает, если не провести дефибрилляцию.

Ревербератор в однородной двухмерной системе возникает, например, при наличии отверстия, периметр которого превышает длину волны l = Vt (V – скорость) распространения волны.

Циркуляция волны возбуждения (ревербератор) возможна и в непрерывной среде, неоднородной по рефрактерности. Если в некоторую область среды, имеющую форму кольца, послать импульс, то он будет циркулировать, т.к. волны возбуждения, распро-страняющиеся по часовой стрелке и против нее, встретятся и погасят друг друга. Если рефрактерность не всюду одинакова, то циркуляция возникает вследствие трансформации (изменения) ритма.

27. МОДЕЛИРОВАНИЕ БИОФИЗИЧЕСКИХ ПРОЦЕССОВ

Метод моделирования является универсальным, применяемым практически во всех областях человеческой деятельности: науке, технике, экономике, медицине, архитектуре. Моделирование – основной метод био-физики. Он применяется на всех уровнях изучения живых систем, начиная от молекулярной биофизики, биофизики мембран, клетки, органов и кончая биофизикой сложных систем. Некоторые модели нами изучены в курсе биофизики. Это уравнение Ходжкина – Хаксли, модель мышечного сокра-щения, кровеносной системы и др.

При изучении сложных систем исследуемый объект может быть заменен другим – более простым, но сохраняющим основные, наиболее существенные для данного исследования, свойства. Такой объект исследования называется моделью. Модель – это всегда некоторое упрощение объекта исследования (его структуры, сложности связей, как внутренних, так и внешних).

На моделировании базируется любой метод научного исследования (теоретического, прикладного).

27.1. Этапы моделирования

1. Первичный сбор информации.

2. Постановка задачи и цели.

3. Обоснование основных допущений.

4. Создание модели, ее исследование.

5. Оценка адекватности модели реальному объекту. Границы применимости модели.

Модели бывают:

1. Физические (модель течения крови).

2. Биологические (гигантский аксон кальмара).

3. Математические (система дифференциальных уравнений).

27.2. Модель естественного роста численности популяции

Реальная система: Имеется некоторая популяция

Постановка задачи. Найти законы изменения численности популяции во времени.

Допущения:

1. Хищники отсутствуют.

2. Внутри вида нет борьбы за место обитания.

3. Размножение и естественная гибель, скорость их пропорциональна численности особей в данный момент.

Модель:

x – численность популяции в момент t.

R – скорость размножения.

g – коэффициент размножения.

S – скорость естественной гибели.

dx/dt – скорость изменения численности популяции.

e – коэффициент роста.

R = gx, S = – sx.

Уравнение баланса

Изменение численности особей в единицу времени определяется количеством рожденных за это время и умерших:

dx/dt =(g -s)х или dx/dt =eх

Начальное условие:

при t=0 x =x_о

Интегрируем

х t

ò (dx/dt) =ò e dt

х_о о

ln(x/x_o) = et

x = x_o e ^et

e < 0	e >0
x     xo t	x   xo       t

Рис.54. Изменение численности популяции во времени

Анализ

1. e < 0 (при s >g) – скорость гибели больше скорости размножения, численность падает до нуля.

2. e > 0 (при g >s) – скорость размножения больше скорости гибели. Неограниченный рост со временем.

3. e = 0 (g =s). Численность неизменна.

Модель при e > 0 адекватна реальности лишь до определенного вре-мени. При большом количестве особей появляется борьба внутривидовая за место обитания – пищевые и водные ресурсы, генетический отбор.

27. 3. Модель изменения численности популяции

с учетом конкуренции между особями

Усложненная модель. Пусть существует внутривидовая борьба между особями, например, за место обитания.

Пусть скорость гибели за счет конкуренции пропорциональна вероятности встречи двух особей, тогда

S = –dx x – sx,

где s- коэффициент пропорциональности.

Уравнение баланса

dx/dt = gх – sх – dх²

тогда, dx/dt=eх – dх² (нелинейное дифференциальное уравнение).

Заменяя U= (e – dх)/х, с учетом, что при t = 0 x = x_o , получим

ln(x/x_o) – ln[(e – dx)/(e – dx_o)] = et,

отсюда

x(t) = {(x_o/e)/[(e – dx_o)e ^–et +dx_o]}

при t ® ¥ х ® х_ст, х_ст = e/d,

где х _ст – стационарный уровень.

х хст   хо   t	Модели 1 и 3 являются осно-вой моделирования процессов в биотехнологии (например, для установления оптимальных режи-мов выращивания различных микроорганизмов), развития эпи-демий.
Рис.55. Изменение численности популяции во времени с учетом конкуренции между особями

27.3. Модель “ хищник – жертва”

Пусть живут два вида особей: зайцы (жертвы) и рыси (хищники).

Зайцы питаются растительной пищей (пищи достаточно), внутривидо-вая борьба отсутствует.

Рыси питаются только зайцами.

х – число жертв в момент времени t.

y – число хищников в момент времени t.

Уравнение баланса между численностью рожденных и гибнущих особей.

Жертвы:

dx/dt = gx - sx - axy

gx - скорость размножения, sx - скорость естественной гибели, axy- скорость гибели за счет встречи с хищником.

Хищники:

dxy – скорость размножения, by – скорость естественной гибели.

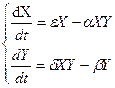(27.1)

Находим стационарное решение x = const, y = const:

dx/dt =0 dy/dt =0.

Система дифференциальных уравнений сводится к алгебраическим:

х_ст(e - aу_ст) =0;

y_ст (dх_ст - b) =0.

Решения:

х _ст =b/d;

Y_ст =e/a.

Предполагая, что произошли малые отклонения численности хищников V(t) и жертв U(t) относительно стационарных значений, имеем

х = х_ст +U(t), U<x _ст , U <Y_ст.

Y =Y_ст +V(t), V <Y_ст, V < X_ст.

dU/dt = X_ст (e – aY_ст) + U (e – aY_ст) – aX_ст V – aUV,

dV/dt = Y_ст (d X_ст – b) + V (dX_ст – b) + dU Y_ст +dUY

или

dU/dt = X ²_ст [– aV/X_ст – (aU/X_ст)(V/X_ст)],

dV/dt = Y²_ст [d(U/Y_ст) + (d U/Y_ст)(V/ Y_ст )].

Пренебрегая членами второго порядка, с учетом (27.1) получим систему уравнений:

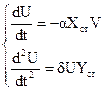, (27.2)

которую сводим к дифференциальным уравнениям второго порядка

d²U/dt² +ebU = 0

и

d²V/dt² +ebV = 0.

Это уравнения колебательных процессов.

Решения уравнений:

U = U_max sin 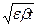, V = V_max sin( 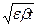+j _o)

Амплитуды относятся:

V_max /U_max = d/a Öe/b.

В результате численности особей при малых отклонениях от стационарных значений равны:

X(t) = X_ст + U_max sin ;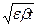

Y(t) = Y_ст + V_max sin(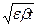 +j _o )

Таким образом, численности популяций X и Y изменяются по синусо-идальному закону, колеблются около стационарных значений с частотой w = (e b)^1/2 и смещены по фазе на j_o. Обнаружена очень большая сходимость с опытными данными за период с 1845 по 1935 годы. Периодичность наблюдается примерно через 10 лет со смещением по фазе примерно на 1,5 года.

27.4. Фармакокинетическая модель

Для описания кинетики изменения концентрации введенного в организм лекарственного препарата предложена фармакокинетическая модель.

Необходимо найти законы изменения концентрации лекарственного препарата при различных способах и параметрах его введения и выведения.

В реальных условиях ввод и вывод лекарства сопровождаются большим числом разнообразных процессов. Это процессы всасывания в кровеносное русло при внесосудистом введении, перенос лекарства из крови к органам, удаление препарата из крови почками и другими органами.

Допущения:

1. Не рассматривается система органов, через которые последо-вательно проходит лекарство. Исключается многостадийность процессов ввода, переноса, вывода лекарственного вещества.

2. Не учитывается молекулярные механизмы процессов (проница-емость вещества, химические превращения).

3. Процессы ввода и вывода определяются скоростью.

Модель:

Существуют различные способы введения лекарственного вещества в организм. Законы изменения концентрации лекарственного вещества во времени C(t):

Однократное введение лекарственного препарата. Пациенту сделан укол.

mo Р   Организм	Представим себе орга-низм как систему объемом V. После введения в эту систему лекарственного пре-парата массой mo, начина-ется его удаление из орга-низма по схеме (рис.56).
Рис. 56. Однократное введение лекарствен- ного препарата

Распределение препарата по объему предполагается равномерным. Скорость удаления препарата Р из организма прямо пропорциональна его массе в организме:

P = – km

k – коэффициент удаления препарата из организма.

Скорость изменения массы лекарственного вещества в организме (dm/dt) равна скорости его выведения Р:

(dm/dt) = Р, и, следовательно, (dm/dt) = – km.

Решение этого дифференциального уравнения с учетом начального условия при t = 0, масса введенного лекарства m = m_o.

m = m_o e ^-kt.

Концентрация лекарственного препарата в организме (например, в крови) c = m/V.

c = (m_o/V) e ^–kt или С = С_о e ^–kt,

где V – объем крови; С_о – начальная концентрация.

С Со     t	Концентрация лекарственного препарата в крови будет непре-рывно снижаться по убывающему экспоненциальному закону (рис.57). При однократном способе введения лекарства не удается поддерживать в крови его постоянную концентрацию.
Рис.57. Изменение концентрации лекарства в организме при однократном способе введения

Второй способ. Непрерывное введение препарата с постоянной скоростью. Пациенту поставлена капельница.

В этом случае изменение массы лекарственного препарата в организме dm/dt определяется не только скоростью его удаления Р, но и скоростью введения (рис.58). Q – количество лекарственного вещества, введенного в организм за единицу времени:

Q Организм Р

Рис.58.Непрерывное введение препарата с постоянной скоростью

(dm/dt) = Q – km.

Получим решение с учетом того, что при t = 0, m = 0:

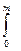[ dm/(Q – km)] = 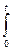dt.

Введя новую переменную U= Q – km,

dU = – km, dm = – dU/k.

ò [dm/(Q – km)] = –(1/k)ò dU/U,

получим

ln (Q – km)/Q = –kt

и, наконец, –

m (Q/k)(1 – e ^–kt).

Концентрация лекарства в крови

C = (Q/kV)(1 – e ^–kt).

В начальный момент времени, при t = 0, С = 0, t ® ¥

e ^–kt ® 0 и С ® Q/kV.

Через некоторое время после начала введения лекарства устанавливается постоянная концентрация:

С = Q/kV.

Подбором скорости введения лекарств Q = kVС_опт добиваются, что через некоторое время устанавливается оптимальная концентрация С_опт, которая необходима для терапевтического эффекта. При непрерывном способе введения лекарства удается достигнуть заданного результата С = С_опт только через некоторое время (рис.59).

С   Сопт     t	Оптимальная концентрация мо-жет быть установлена мгновенно при сочетании первого и второго спосо-бов.
Рис.59. Достижение оптимальной кон- центрации лекарственного препарата в организме при непрерывном введении

Третий способ. Состояние непрерывного введения лекарственного препарата (первый способ) с введением нагрузочной дозы (второй способ).

Сопт   t	m0   QP
Рис.60. Комбинированный способ введения лекарственного препарата

В этом случае фармакокинетическая модель имеет вид

С=(Q/kV) – (1/V)(Q/k – m_o)e ^–kt.

С = С_опт.

Если скорость введения лекарства (капельницей)

Q=kVC_опт

и нагрузочная доза

m_o=(Q/k)=VC_опт,

то постоянная концентрация устанавливается мгновенно.

Фармакокинетическая модель дает возможность рассчитать оптимальное соотношение между параметрами ввода и вывода препарата для достижения терапевтического эффекта.