Основы мышечного сокращения

Теория мышечного сокращения В.И. Дещеревского (1968 – 1977) основана на следующих положениях:

1. Каждый поперечный мостик в процессе сокращения проходит последовательно через три состояния:

а) свободное (разомкнутое) состояние около некоторого положения равновесия на толстой нити;

б) тянущее состояние во время которого возникает сила f_э;

в) тормозящее замкнутое состояние, которое препятствует дальнейшему скольжению нити.

За состоянием (в) следует состояние (а), как показано на рис.26.

2. Элементарная сила f_э постоянна и положительна (направлена к центру саркомера) в тянущем состоянии.

В тормозящем замкнутом состоянии сила имеет обратное по знаку, тоже по абсолютной величине значение.

а б

fэ fэ (+)   0 d     fэ (-)	k1 g n   k2 k= u/ d   m
Рис.26. а – направление fЭ; б – последовательность состояний саркомера

3. Для любого данного мостика переходы между состояниями не зависят от состояния других мостиков, т.е. можно назвать эти процессы мономолекулярными.

Весь цикл функционирования мостика можно представить в виде последовательных реакций первого порядка, происходящих с присущими им скоростями.

Константы скорости этих процессов могут зависеть от скорости скольжения нитей. Известно, что константы скорости превращения первого порядка –величина обратная времени, в течение которого данная структура существует до момента превращения. Время жизни мостика в тянущем состоянии определяется: d /u, где d – путь, проходимый мостиком в тяну-щем состоянии, u – скорость движения нитей относительно друг друга.

Для константы скорости перехода мостика в тормозящее состояние справедливо соотношение:

.

Время жизни мостика в свободном состоянии 1/k, и константу скорости замыкания k₁ можно считать независимой от u. Действительно, мостик замыкается только тогда, когда перед ним находится активный центр тонкой нити в благоприятном для замыкания состоянии, и он сам в этот момент также должен быть готов к этому процессу. Оба эти события напрямую не связаны со скоростью перемещения нитей в саркомере. Однако, время пребывания данного центра тонкой нити перед мостиком уменьшается с повышением значения u, поэтому снижается вероятность за-мыкания мостика на этом центре. Но в то же время с ростом u увели-чивается число активных центров, находящихся вблизи мостика за время 1/ k₁. Считают, что свободный мостик имеет в среднем примерно одно и то же время для замыкания на средне статистическом активном центре тонкой нити.

4. f_э и k₂ зависят от скорости скольжения нитей, то есть процесс раз-мыкания происходит, в силу особых свойств комплекса мостика, по случай-ному закону за время 1/k₂.

Движение толстых и тонких нитей в саркомере (скольжение одной относительно другой) происходит относительно середины его длины. Поэтому при описании процесса удобно пользоваться величиной, состав-ляющей половину этой длины (полусаркомер). Две половины саркомера при сокращении волокна движутся навстречу друг другу, скорость укорочения саркомера равна удвоенной скорости укорочения полусаркомера, который укорачивается со скоростью скольжения нитей U.

В мышечном волокне саркомеры следуют один за другим (после-довательное соединение). Скорость укорочения мышечного волокна сос-тавляет сумму скоростей укорочения всех саркомеров:

V₁ = 2NU, (15.1)

где N – число саркомеров в мышечном волокне, 2U – скорость укорочения саркомера.

Сила на концах мышечного волокна образуется за счет положительных элементарных сил в мостиках в тянущем состоянии и отрицательных сил, возникающих в мостиках при тормозящем состоянии.

Если общее число мостиков в полусаркомере находящемся в данный момент в тянущем состоянии, n, а в тормозящем m, то равнодей-ствующая сила

f = nf_э – mf_э. (15.2)

Согласно второму закону Ньютона, сила, развиваемая мышцей:

F = m a + P n, (15.3)

где m – масса нагрузки, а – ускорение, Р – внешняя сила (например, вес). То же справедливо и для мышечного волокна, т.е. сила f, развиваемая мышечным волокном, вызывает движение нагрузки с ускорением dV/dt c преодолением внешней силы Р₁.

Поэтому можно записать:

(n -m)f_э = 2m₁N dU/dt + H₁ (15.4)

или через ускорение:

dU/dt = 1/ 2m₁N [(n – m)f_э – P₁]. (15.5)

Скорость изменения числа мостиков в замкнутом тянущем состоянии dn/dt, согласно закономерностям кинетики процессов первого порядка,подчиняются уравнению

dn/dt = k₁ g – kn, (15.6)

где g – число мостиков в разомкнутом состоянии.

Принимая во внимание, что k=U/ d и суммарное число мостиков в зоне одинарного перекрывания толстых и тонких нитей полусаркомера a = g + m + n, можем записать

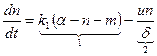. (15.7)

Первый член (15.7) – это скорость перехода в тянущее состояние из равновесного разомкнутого, второй – скорость перехода мостиков в тормозящее состояние.

Для скорости изменения числа мостиков в тормозящем состоянии записывается аналогично:

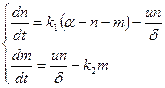, (15.8)

Полученная система дифференциальных уравнений дает возможность рассчитывать необходимые параметры мышечного волокна.

Кинетические кривые изотонического укорочения портняжной мышцы лягушки изображены на рис.27.

а

x,м

0,2 1 _* 2_{. *}3 x – укорочение,

_{*. *} t – время от начала стимула.

_{*. *.} . 4

0,1 _{*. *.}

_{*. *.}

t_o 0,1 0,2 0,3 t,с

б

1– Тянущее замкнутое состояние

2 – Свободное разомкнутое состояние

3 – Тормозящее замкнутое состояние

Рис.27. а – Кинетические кривые изотонического укорочения портняжной

мышцы лягушки; б – три состояния саркомера.

16. БИОФИЗИКА КРОВООБРАЩЕНИЯ

Система кровообращения является гидродинамической. Сердце живого организма (человека) работает периодически, посылая кровь по сосудам. Поэтому движение и давление крови имеет колебательный характер. Сложность описания полной системы кровообращения физико-математическими методами заключается в том, что свойства сосудов (упругость стенки) изменяется на протяжении сосудистого русла.

Биофизические исследования, в связи с вышесказанным, идут по двум основным направлениям.

1. Изучение физических процессов, определяющих движение крови по сосудам.

2. Анализ движения крови в отдельных сосудах или их совокупности.

Рассматривают процесс на гидродинамической модели кровообра-щения.

При движении крови по сосудам, имеющим активное сопротивление, происходит потеря энергии за счет работы по преодолению этого сопротивления, то есть имеют место инерционность при распространении импульсов и другие факторы, характерные для электрических цепей. Поэтому систему кровообращения моделируют аналоговыми электрическими цепями.

Кровь, как любая жидкость, имеет определенную вязкость h. Вязкость это коэффициент пропорциональности между напряжением сдвига s и градиентом скорости движения жидкости. Если градиент скорости не равен нулю только в одном направлении х, то можно записать для однонап-равленного течения s = h du/dx. Напряжение сдвига s_c = f_c/s, где f_c – сила сдвига, приложенная к площадке s. Вектор f лежит в плоскости s, u – скорость движения жидкости при ее ламинарном течении на расстоянии х от плоскости s, du/dx – грдаиент скорости движения (скорость деформации сдвига). С помощью такого уравнения описывают движение Ньютоновских жидкостей. Для крови это уравнение не подходит т.к. при расчете по этому уравнению вязкость крови (эффективная вязкость) резко падает с увеличением скорости сдвига.

Для скоростей сдвига меньших 100 с, в случае течения крови, лучшую сходимость с опытными данными имеет уравнение Кессона, полученное эмпирическим путем:

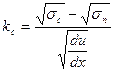, (16.1)

где s_n (константа) – предел текучести. Кровь приходит в движение при s_c >s_n, то есть параметр k_c>0, значение его для крови 0,05-0,15 Па^0.5 с^0.5, а s_n составляет 0,01-0,05 н/м².

Кровь h 0,4 -– Нютоновская жидкость 0,2 – | | | 1 10 100 du/dx,c-1

Рис.28. Зависимость вязкости от скорости сдвига

Для высоких значений напряжения сдвига s_c >>s_n это уравнение превращается в уравнение для Ньютоновских жидкостей, в котором

h =k_c ². (16.2)

16.2. Движение крови по кровеносному руслу

Кровь – неоднородная жидкость. Она содержит в своем составе различные клетки. Для крупных кровеносных сосудов кровь можно рассматривать как суспензию эритроцитов и других клеток в физиологическом растворе. Для тонких капилляров необходимо учитывать не только концентрацию клеток, но и их физические свойства.

Вязкость суспензии резко увеличивается при повышении концентрации суспензионных частиц (рис. 29). Благодаря дисковидной форме клеток и эластичности оболочки эритроцитов ее суспензия обладает сравнительно невысокой вязкостью, и уменьшается нагрузка на сердце (насос).

При патологических процессах увеличивается жесткость стенок эритро-цитов, что приводит к увеличению вязкости крови и ухудшению кровообращения. Рассмотрим движение цилиндрического элемента крови с высотой dx в кровеносном сосуде цилиндрической формы с радиусом r.

h h/ hс 6 - 4 - 2 -     20 40 60 С,%
Рис.29. Зависимость вязкости суспензии от ее концентрации

Движение такого элемента обусловлено разностью давлений dp –частный дифференциал. Все другие переменные const. Сила при этом будет равна f = – p r² dp.

x dx 2r 2r P1 P2 h     Рис.30 . Движение элемента крови по сосуду

Элемент обладает массой   dm= r Sdx . Sdx = pr2, где dx – объем, r – плотность кро-ви. Он движется со средней ско-ростью u и имеет ускорение du/dt. Тогда для случая, когда сила тяжести не учитывается, выраже-ние второго закона Ньютона мо-жем записать:

– Sdp = dm ^. du/dt+df. (16.3)

Если принять, что вязкое движение крови по сосуду подчиняется закону Пуазейля, сила

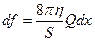, (16.4)

где Q – расход крови, то есть объем крови, протекающий через сечение сосуда в единицу времени. Подставим полученное уравнение в (16..3), заменим отношения дифференциалов на частные производные, поделим на S и dx и получим искомое уравнение:

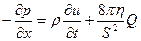. (16.5)

Кровь течет по сосудам, пульсируя. Сердце выталкивает в крупные кровеносные сосуды порцию крови. В результате эластичности стенок сосудов они при повышении давления на некотором участке подвергаются пластической деформации. Происходит расширение данного участка. Упру-гие свойства стенок сосуда развивают силу, приводящую к восстановлению первоначальных параметров сосуда, а порция крови проталкивается в соседний участок, на котором все описанное повторяется, и т.д.. Таким образом, по сосуду распространяется импульс давления, скорости кровотока и деформации сосудистой стенки.

Скорость распространения пульса намного выше средней скорости течения крови.

Пусть деформация сосуда происходит за время dt. Уравнение деформации при высоком модуле упругости стенки сосуда имеет вид:

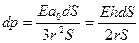, (16.6)

где E – эффективный модуль упругости стенки сосуда, a_o = rh, h – толщина стенки сосуда, a_o = rh. Поделив на dt, получим частный дифференциал по времени:

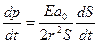(16.7)

Объем участка длиной dx за время dt за счет расширения сосуда увеличивается на dSdx. Кровь – несжимаемая жидкость и течет по сосудам неразрывной струей. Изменение объема втекающего в участок dx (Q₁dt) и вытекающего в соседний участок (Q₂dt) будет:

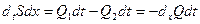, (16.8)

где d_xQ – изменение объемной скорости кровотока по длине сосуда.

Это уравнение можно переписать:

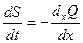. (16.9)

Если подставить это уравнение в уравнение деформации получим:

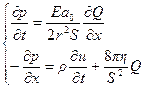(16.10)

Это уравнение в совокупности с ранее приведенным уравнением образуют систему, которая отражает взаимозависимость давления и объемной скорости кровотока и описывают их изменение по ходу сосуда и во времени. Сокращение сердца вызывают выброс крови в кровеносное русло. Это сопровождается периодическим изменением давления, которое можно описать, как любой периодический процесс, с помощью некоторой суммы гармонических колебаний с частотой nn_о, n – натуральные числа, n_о – частота 1Гц.

Разложение сложного гармонического колебания на составляющие называется Фурье-анализом. Для определения распространения суммарных естественных пульсовх волн надо определить их составляющие, а затем, суммировав, перейти к искомой величине. Пусть давление р в точке х= 0 изменяется по гармоническооку закону с круговой частотой w =2pnР(0) = Р_о cos w t.Тогда решение системы дифференциальных уравнений будет уравнением затухающей волны:

Р = А_ое^ccos(wt – bх). (16.11)

Коэффициенты c и b связаны с R,L и С соотношениями

b² – c² = w²LC; 2bc = wRC, (16.12)

*.... ¦.*... ' ' - ¦. *. ' '.. ' ¦..*' '..' ¦ ' '. *. '. * t,с ¦ ' '.. * ' '.* - ¦.. * *. ¦ * *	А0 – максимальная амплитуда коле-баний давления: А0 = Р при cos(w t – b х ) = 1 и х = 0. Коэффициент c показывает на скорость затухания по ходу сосуда. Амплитуда колебаний в точке х равна Аоexp(– c x) – уменьшается по ходу сосуда по экспоненциаль-ному закону.
Рис.31. Разложение сложного колеба- ния на составляющие

Величина b х – сдвиг фаз. b связан со скоростью распространения волны V и с ее длиной l соотношениями:

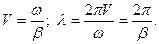(16.13)

Если сопротивление току крови в основном определяется инерционностью (w L <<R), то скорость приближенно будет

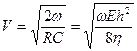(16.14)

то есть фазовая скорость распространения упругих волн увеличивается с частотой.

Если сопротивление току крови в основном определяется инерционностью (wL>>R), что характерно для крупных сосудов, выражение для скорости будет другим:

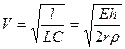.(16.15)

Зависимости от частоты нет, то есть все гармонические слагаемые сложного колебания (пульса) распространяются по сосудам с одинаковой скоростью.

Кровеносных сосуды и кровоток изучают с помощью анализа распространения искусственных гармонических волн давления на подопытных животных. Эти волны генерируются электромагнитным ударником, вызывающим периодические изменения площади просвета и давления. Амплитуда генерируемой волны Р не должна быть большой (~ 100Па), чтобы такая волна не влияла на естественное течение крови и стабильно регистрировалась приборами на фоне естественного импульса давления.

ЭМУ Д2 Насос Д1	Датчики, находящиеся на рас-стоянии х друг от друга, фиксируют давление (амплитуды давления), определяя время, находят фазовую скорость распростране-ния волны V=x/t. С помощью таких опытов было подтверждено, что фазовая скорость практически не зависит от частоты и затухание волны давления по ходу русла имеет экспоненциальный характер.
Рис.32. Схема установки для изучения кровотока

Линейная теория кровотока по упругим сосудам может быть использована для измерения скорости распространения пульса, определения на этой основе модуля упругости сосудистой стенки.

По измеренным давлениям двух близко расположенных участков сосуда при известных R и L можно рассчитать импульс объемного расхода крови.