Неравенство Клаузиуса

Совместное применение первой и второй теорем Карно позволяет получить следующее неравенство:

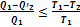
Знак равенства в этой формуле соответствует случаю описания обратимой тепловой машины, а знак меньше - описанию необратимой тепловой машины.

Формулу можно преобразовать к виду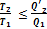

Это выражение в свою очередь дает 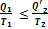или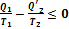

Если полученное выражение записать через количество теплоты, подводимой к рабочему телу от нагревателя 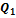и холодильника 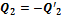, то оно примет окончательную форму

Эта формула представляет собой частный случай неравенства Клаузиуса.

Для получения неравенства Клаузиуса в общем случае рассмотрим тепловую машину, рабочее тело которой при совершении кругового термодинамического процесса обменивается теплотой с достаточно большим числом тепловых резервуаров (нагревателей и холодильников), имеющих температуры 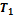, ,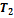..., 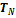(см. рис). При этих теплообменах рабочее тело получает от тепловых резервуаров теплоты 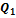, ,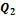..., . 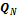Работа такой тепловой машины будет равна: 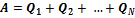. При использовании этого выражения необходимо учитывать, что теплоты 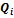могут иметь отрицательный знак в случае, если в при теплообмене с -тым резервуаром теплота отбирается от рабочего тела.

Схема тепловой машины с большим числом нагревателей и холодильников

Применительно к рассматриваемой тепловой машине неравенство может быть записано в виде

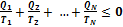или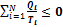

Величина называется приведенным количеством теплоты, которое численно равно количеству теплоты, полученной системой, при абсолютной температуре 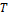, деленной на эту температуру.

При переходе к бесконечному числу тепловых резервуаров, с которыми рабочее тело тепловой машины обменивается теплотой, суммирование в формуле может быть заменено интегрированием по замкнутому термодинамическому циклу: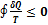

Из этой формулы следует, что сумма приведенных количеств теплоты на замкнутом цикле для любой термодинамической системы не может быть больше нуля. Неравенство было получено в 1862 году Клаузиусом и носит его имя.

Неравенство Клаузиуса позволяет отличать обратимые и необратимые круговые термодинамические процессы. В случае, если термодинамический цикл состоит только из обратимых процессов, неравенство переходит в равенство Клаузиуса , имеющее принципиальное значение для построения равновесной термодинамики.

Случай строгого неравенства в формуле соответствует описанию необратимых круговых термодинамических процессов, и это выражение применяется в неравновесной термодинамике.

Статистическое толкование закона возрастания энтропии.

Рассматривая Вселенную как изолированную систему и распространяя на неё второй закон термодинамики, Р. Клаузиус пришёл к выводу о неизбежности «тепловой смерти» Вселенной, при которой в необозримом будущем в ней будет достигнуто состояние термодинамического равновесия и всякие процессы прекратятся. Этот вывод вызвал много споров, которые не прекращаются до сих пор. К Вселенной в целом как изолированной системе (F = 0) второе начало термодинамики неприменимо по определению. В силу этого предсказанная Р. Клаузиусом «тепловая смерть» вследствие непрерывного возрастания энтропии ей не угрожает. Понятие энтропии приложимо исключительно к открытым (неизолированным) термодинамическим системам.

Напомним, что ни классическая, ни современная термодинамика не отрицают применимости второго начала к изолированным системам и в силу этого принципиально не могут противостоять упомянутому выше утверждению Клаузиуса достаточно решительно. Они опираются на статистическое истолкование второго закона с помощью формулы Больцмана: S = k ln W, W – число способов, которым может быть реализовано данное конкретное состояние (число возможных расположений частиц в теле). При этом второй закон термодинамики формулируется следующим образом: природа стремится от состояния менее вероятного к состоянию более вероятному.

Связь между S и W позволяет несколько иначе сформулировать второе начало термодинамики: наиболее вероятным изменением энтропии является ее возрастание.

Энтропия – вероятностная статистическая величина. Утверждение о возрастании энтропии потеряло свою категоричность. Её увеличение вероятно, но не исключаются флуктуации*.

Поскольку все реальные процессы необратимы, то в случае их прохождения в изолированной системе ее энтропия всегда будет увеличиваться.

Принцип возрастания энтропии имеет большое практическое значение:

1. Он указывает на направление протекания процессов. Самопроизвольные процессы, приводящие систему к равновесному состоянию, идут в направлении возрастания энтропии системы. Следовательно, если система находится в неравновесном состоянии, то ее энтропия возрастает ΔS_С>0.

2. Дает возможность судить о глубине самопроизвольных процессов. Такие процессы идут до достижения максимума энтропии системы S_С=S_СМАХ. Следовательно, если система находится в равновесном состоянии, то ее энтропия не изменяется ΔS_С=0. Энтропия замкнутой системы – максимальна, при достижении системой равновесного состояния.

3. Увеличение энтропии системы может служить мерой необратимости протекающих в ней процессов, т.е. второй закон термодинамики дает не только качественную, но и количественную оценку процессов.

Таким образом, являясь статистическим законом, второй закон классической термодинамики выражает закономерности хаотического движения большого числа частиц, входящих в состав изолированной системы. Для систем с относительно малымили бесконечнымчислом частиц второй закон термодинамики неприменим: в первом случае из-за возможных значительных флуктуаций, во втором — из-за равновероятности всех микросостояний

* Флуктуа́ция (от лат. fluctuatio — колебание) — термин, характеризующий любое колебание или любое периодическое изменение.

49. Объединенный закон термодинамики.

В природе одновременно действуют две тенденции - стремление к минимуму энергии, и стремление к максимуму хаоса, т.е. одновременно действуют первый и второй законы термодинамики. И чтобы описать результат их совместного действия, нужны критерии, учитывающие сразу обе тенденции. Иными словами, нужно объединить первое и второе начала термодинамики.

Рассмотрим круговой процесс, у которого процесс 1-а-2 протекает необратимо, а процесс 2-b-1 - обратимо. Представим круговой интеграл в виде суммы двух линейных интегралов с учетом .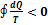

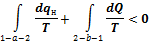
Второй интеграл равен разности энтропий , тогда можно написать 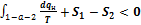, или 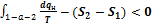. Таким образом, 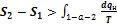. Чем выше степень необратимости, тем больше разность между 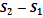и .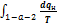

Представим 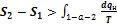в дифференциальной форм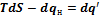е , где по Клаузиусу - нескомпенсированная теплота превращения. Используя дифференциальную форму, можно написать

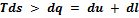, откуда 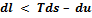, т.е. работа, совершенная системой в необратимом процессе, меньше, чем при обратимом.

В общем случае объединенный закон термодинамик и можно представить в виде 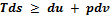, где знак равенства относится к обратимым, а знак неравенства - к необратимым процессам.

Однако эти неравенства не позволяют количественно определить влияние необратимости на эффективность ТС. Поэтому вернемся к уравнению 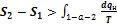и перепишем его в виде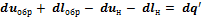

Так как оба процесса характеризуются одинаковыми состояниями в точках 1 и 2, то 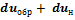, тогда 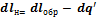. Следовательно, теперь объединенный закон термодинамики примет вид .

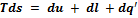Для обратимых процессов.

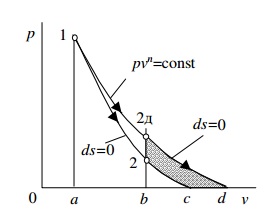
Применим 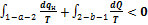к примеру, показанному на рис. 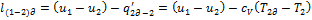, то есть чтобы вернуть ТС из состояния, определяемого точкой 2д в состояние 2, необходимо от ТС отвести теплоту 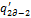, при этом идеальная работа расширения также уменьшится на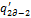

Для адиабатической системы (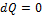) из 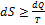получим .

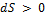Это условие показывает, что если в адиабатической системе протекают любые обратимые процессы, то энтропия системы остается неизменной (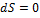). Протекание реальных процессов, которые всегда необратимы, сопровождается увеличением энтропии системы (), то есть ТС переходит только в такое состояние, при котором .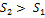

Отметим, что большинство энергетических машин и установок, в которых имеет место незначительный теплообмен с окружающей средой, можно мысленно заключить в адиабатическую оболочку и рассматривать их как открытые адиабатические термодинамические системы. Такое допущение существенно упрощает термодинамический анализ реальных систем.

50. Реальный газ. Уравнение Ван – дер – Ваальса.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона: 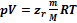, где p — давление; V — объем; T — температура; Z_r = Z_r (p,T) — коэффициент сжимаемости газа; m — масса; М — молярная масса; R — газовая постоянная.

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия U становится функцией не только температуры, но и объёма.

Уравнение Ван-дер-Ваальса — это одно из широко известных приближённых уравнений состояния, имеющее компактную форму и учитывающее основные характеристики газа с межмолекулярным взаимодействием.

Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальс (1837—1923) вывел уравнение состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.

1. Учет собственного объема молекул. Наличие сил отталкивания, которые проти­водействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V _m, а V _m — b, где b — объем,занимаемый самими молекулами.

Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в рас­чете на одну молекулу.

2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислени­ям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату моляр­ного объема, т. е. 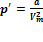, где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного при­тяжения, 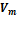— молярный объем.

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):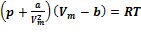

Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vV_m, уравнение Ван-дер-Ваальса примет вид 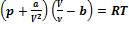, или 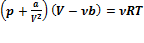, где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).

При выводе уравнения Ван-дер-Ваальса сделан целый ряд упрощений, поэтому оно также весьма приближенное, хотя и лучше (особенно для несильно сжатых газов) согласуется с опытом, чем уравнение состояния идеального газа.