 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойство 10 означает, что каждое действительное число принадлежит по крайней мере, одному из множеств и
|
|
Из свойства 30 следует, что множества  и
и 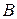 не пересекаются:
не пересекаются: 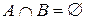 .
.
Сечение множества действительных чисел, образованное множествами  и
и 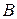 обозначается через
обозначается через  .
.
Множество  называется нижним классом, а множество
называется нижним классом, а множество 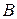 – верхним классом данного сечения.
– верхним классом данного сечения.
Пусть 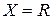 . Простые примеры сечения в множестве действительных чисел можно получить следующим образом. Зафиксируем какое-либо число
. Простые примеры сечения в множестве действительных чисел можно получить следующим образом. Зафиксируем какое-либо число  , то множества
, то множества
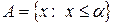 и
и 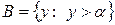 , (1)
, (1)
а также
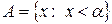 и
и  (2)
(2)
образуют сечения множества 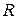 .
.
В обоих этих случаях говорят, что сечение  производится числом
производится числом 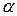 и пишут
и пишут 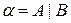 .
.
Отметим свойства сечений, производящихся некоторым числом.
1. В случае (1) в классе  есть наибольшее число
есть наибольшее число 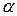 , а в классе
, а в классе 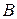 нет наименьшего числа. В случае (2) в классе
нет наименьшего числа. В случае (2) в классе  нет наибольшего числа, а в классе
нет наибольшего числа, а в классе 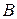 есть наименьшее число, им является число
есть наименьшее число, им является число 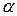 .
.
Доказательство. Рассмотрим, например, случай (1). То, что 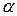 является наибольшим числом в классе
является наибольшим числом в классе  , следует из первой формулы (1), задающей множество
, следует из первой формулы (1), задающей множество  .
.
Покажем, что во множестве 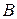 нет наименьшего числа. Допустим противное: пусть в
нет наименьшего числа. Допустим противное: пусть в 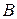 есть наименьшее число
есть наименьшее число  . Из условия, что
. Из условия, что  , следует, что
, следует, что  . Следовательно,
. Следовательно,  , т.е.
, т.е. 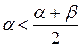 . Отсюда, в силу определения множества
. Отсюда, в силу определения множества 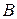 , получаем, что
, получаем, что  . Аналогично из
. Аналогично из  , следует
, следует 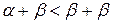 , т.е.
, т.е. 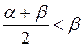 , а так как
, а так как  – наименьшее число в классе
– наименьшее число в классе 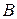 , то
, то  . Полученное противоречие доказывает утверждение.
. Полученное противоречие доказывает утверждение.
2. Число, производящее сечение, единственно.
Доказательство. Допустим противное, что существует сечение, которое определяется двумя разными числами: 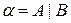 и
и  . Пусть, для определенности
. Пусть, для определенности  . Тогда как было показано при доказательстве предыдущего свойства
. Тогда как было показано при доказательстве предыдущего свойства 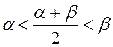 . Из неравенства
. Из неравенства 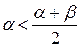 следует, что в случае (1)
следует, что в случае (1)  . Аналогично из неравенства
. Аналогично из неравенства 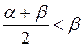 следует, что
следует, что  . Это противоречит тому, что
. Это противоречит тому, что 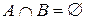 .
.
3. Для каждого сечения  множества действительных чисел существует число
множества действительных чисел существует число 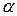 , производящее это сечение:
, производящее это сечение: 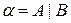 .
.
Это число, согласно доказанному выше, является либо наибольшим в нижнем классе, тогда в верхнем классе нет наименьшего, либо наименьшим в верхнем классе, тогда в нижнем классе нет наибольшего.
Это свойство непрерывности действительных чисел часто называют принципом непрерывности действительных чисел по Дедекинду.
Дата публикования: 2015-09-17; Прочитано: 276 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
