Основные задачи на метод координат

Задача № 1.

Нахождение координат точки в данной системе.

R={O,(e₁,e₂)} – система координарат

"M

^{_______________________________________________}

Найти координаты точки М

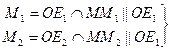_Þ OM₁MM₂ параллелограмм Þ OM=OM₁+OM₂ (1)

OM₁ || OE₁ , т.е. OM₁ || e₁ Þ xÏOM₁ = xe₁ 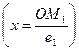(2)

OM₂ || OE₂, т.е. OM₂ || e₂ Þ yÏOM₂ = ye₂ 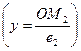(3)

(1), (2), (3) Þ OM = xe₁+ye₂ Þ M (x, y)

Задача № 2.

Обратная задача задачи № 1.

R = { O, (e₁, e₂)} OM₁= xe₁

M (x, y) OM₂ = ye₂

^{________________________}

Построить М

OM = OM₁+ OM₂ (диагональ параллелограмма OM₁MM₂)

M – конец радиус - вектора ОМ

Задача № 3.

Вычисление координат вектора по координатам начала и конца.

R = { O, (e₁, e₂)}

M₁ (x₁, y₁)

M₂ (x₂, y₂)

^{________________________________}

Найти координаты М₁М₂

M₁ (x₁, y₁) Þ OM₁ (x_1, y₁)

M₂ (x₂, y₂) Þ OM₂ (x₂, y₂)

M₁M₂ = OM₂ - OM₁

M₁M₂ = (x₂ - x₁, y₂ -y₁)

Правило: чтобы найти координаты вектора достаточно из координат конца вектора вычесть одноименные координаты начала вектора

Задача № 4.

Деление отрезка в данном отношении.

Прежде чем сформулировать задачу, введем понятие простого отношения 3^х точек прямого.

Пусть М₁, М, М₂ – три точки прямой и М₁ ¹ М₂

Df: простым отношением 3^х точек М₁, М₂, М (М₁, М₂, М)

называют число l такое, что М₁М = l ММ₂

(М₁, М₂, М) = l | М₁М = l ММ₂

Пара М₁М₂ называется основной парой, а т. М – делящая точка

Рассмотрим значение простого отношения 3^х точек при различном расположении т. М (М₁М₂)

В зависимости от положения т. М на прямой (М₁М₂) простое отношение 3^х точек принимает все действительные значения, кроме –1, т.е. l ¹ -1. Если простое отношение 3^х точек равно l и точки М₁ и М₂ различны, то будем говорить, что т. М делит отрезок

[ М₁М₂ ] в отношении l.

Замечание: l > 0, то т. М лежит внутри отрезка, т.е. М делит отрезок внутренним образом; l< 0, то М лежит вне отрезка, т.е. М делит отрезок внешним образом.

R = {O, (e₁, e₂)}

M₁¹ M₂

M₁ (x₁, y₁)

M₂ (x₂, y₂)

(M₁, M₂, M) = l (l ¹-1)

^{____________________________________}

Найти координаты т. М

Обозначим М (x, y)

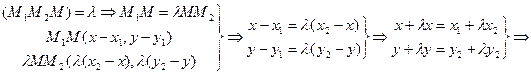
Þ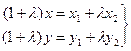

l ¹ -1 Þ (1+l) ¹ 0

Если М- середина [М₁М₂ ]Þ l = 1, тогда 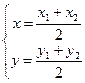(1)

(2)

Из формулы (2) следует, что координаты середина отрезка равныполусуммам одноименных координат его концов.

Задача № 5.

Расстояния между точками.

R = {O, (i, j)}

d = (M₁M₂)

M₁(x₁y₁)

M₂(x₂y₂)

^{_______________________}

Найти d -?

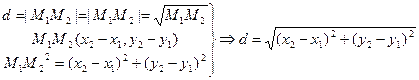
d =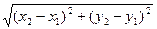

Правило: расстояние между двумя точками, заданными своими координатами в декартовой прямоугольной системе координат, равно корню квадратному из суммы квадратов разности одноименных координат.

Задача № 6.

Площадь треугольника.

R = { O, (i, j)}

D M₁M₂M₃

M₁ (x₁, y₁)

M₂ (x₂, y₂ )

M₃ (x₃, y₃)

^{_____________________}

S _D -?

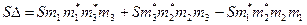
Учитывая, что S_mpan = , перепишем последнее равенство в виде:

S_D =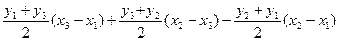

Раскрывая скобки, приводя подобные и перегруппировав, полученные выражения, правую часть приведем к виду:

S_D =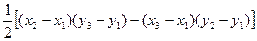

Если поменять местами точки М₁ и М₂, т.е. изменить ориентацию треугольника, то аналогично получим:

S_D = (1)

Df: Табличка из 4^х чисел C = 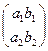, имеющая 2 строчки и 2 столбца, называется квадратной матрицей 2^го порядка (2 x 2 – матрица)

Df: Определитель матрицы 2^го порядка есть число

D = detc =

Используя понятие определителя формулу (1) можно переписать в виде:

S_D = 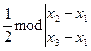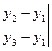(2)

Лекция 6

Преобразование афинной системы координат. Ориентация плоскости.

Пусть на плоскости выбраны 2 афинные системы координат I = R = {O, (e₁, e₂)} и

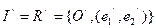, M – произвольная точка плоскости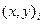: M , M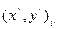

Задача преобразования координат состоит в следующем: зная координаты точки в одной системе координат и параметры, определяющие положения этой системы относительно другой, вычислить координаты т. М в другой системе координат.

Решим задачу преобразования координат, считая известным новые координаты точки

M(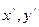) и параметры, определяющие положение новой системы относительно старой

Обозначим: O^’(x₀,y₀)_I

e₁^’(c₁₁,c₂₁)_I

e₂^’(c₁₂,c₂₂)_I

O,O^’,MÞOM=OO^’+O^’M (1)

M(x,y)_IÞOM= xe₁+ye₂ (2)

O^’(x₀,y₀)_IÞOO^’=x₀e₁+y₀e₂ (3)

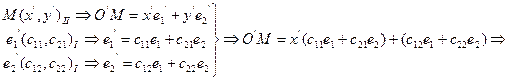
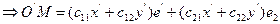(4)

(2), (3), (4) – (1)Þ xe₁+ye₂ = x₀e₁ + y₀e₂ + (c₁₁x^’+c₁₂y^’)e₁ + (c₂₁x^’+c₂₂y^’)e₂ Þ

Þ[x -(c₁₁x^’ + c₁₂y^’+x₀)e₁ ] +[y -(c₂₁x^’ + c₂₂y^’+ y₀)]e₂ = 0

Так как вектора e₁, e₂ образуют базис, т.е. линии независимы, то последнее равенство возможно лишь при условии, когда оба выражения в квадратных скобках, одновременно равны нулю.

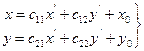(5)

Матрица 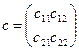называют матрицей перехода от новой системы координат к старой. Ее столбики составлены из координат 1^го и 2^го базисных векторов

D = 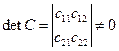(6)

Пусть D = 0Þ с₁₁с₂₂ - с₂₁с₂₂ =0

с₁₁с₂₂ = с₂₁с₂₂

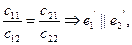что невозможно, т.к. e₁^’ и e₂^’ – базисные вектора 2^ой

системы. Рассматриваем систему (5), как систему 2^х линейного уравнения с 2^мя неизвестными x^’, y^’,и учитывая, что определитель этой системы (6) не равен нулю, мы сможем решить ее относительно x^’, y^’ и получить формулы, выражающие новые координаты т. через старые координаты.

1. Замена базиса.

Пусть системы координат I, I^’ имеют общие начала, но разные базисы, т.е. О^’ = 0

O^’ = O(0,0)_I; x₀ = 0 Ù y₀ = 0

Перепишем формулы (5) в виде:

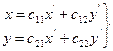(5^’)

(5^’) – формула замены базиса

2. Перенос начала.

I = R = {O, (e₁,e₂)} и I^’ = R^’ = {O^’, (e₁,e₂)}

O^’(x₀,y₀)_I

e₁^’= e₁(1,0)_I

e₂^’= e₂(1,0)_I

Подставим в (5) получим:

(5 ^‘’)