 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Частные случаи преобразования ДПСК
|
|
А). Замена базиса.
R = { O, (i, j)}, R = {O, (i, j) }
O = O (0.0) Þ (x = 0 ^ y = 0)
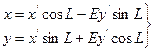 (8*)
(8*)
Б). Поворот осей на угол L
R = { O, (i, j)} и R = {O, (i, j) }, R ^ R –один. ориентир, т.е. E = +1
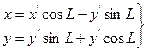 (8**)
(8**)
B). Перенос начала.
R = { O, (i, j)}, R = {O, (i, j) }
O (x, y)  (8*** )
(8*** )
i = i (1, 0)
j = j (0, 1)
Лекция 7
Полярная система координат. Переход от полярной системы к декартовой и обратно.
DF: Полярным репером называется фигура, состоящая из фиксированной точки О и данного вектора е
P = { O, (e) }
полюс орт
Покажем, что полярный репер определяет на плоскости систему координат
Луч (OP) е – полярная ось
М – произвольная точка плоскости, тогда ее положение можно определить 2 числами: r = | OM |, j = POM
Числа r и j - полярные координаты точки М
r – полярный радиус -r = | OM |
j - полярный аргумент j = POM
Чтобы соответствие между полярными координатами и точками плоскости были одинаковы, на полярные координаты накладываются ограничения:
r ³ 0, 0 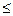 j < 2 p Ú -p
j < 2 p Ú -p 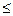 p
p 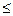 p; M (r, j), M ¹ 0
p; M (r, j), M ¹ 0
Если М = 0, то М (0), а полярный аргумент не определен.
Замечание: помимо рассмотренной полярной системы координат (обыкновенной) иногда рассматриваются обобщения полярные системы координат. Полярный репер определяется точно также, а на полярный радиус и полярный аргумент не накладывается никаким ограничениям.
В полярной системе координат решаются все основные задачи на метод координат:
1. задача нахождения координат точки в данной системе.
2. задача построения точки по ее координатам.
3. задача нахождения координат вектора по полярным координатам его концов.
4. задача деления отрезка в данном отношении.
5. задача нахождения расстояния между 2 точками.
6. задача вычисления площади треугольника.
Чтобы не решать заново все эти задачи, найдем формулу перехода от полярной СК к декартовой.
Переход от полярной системы к декартовой и обратно.
P = { O, (e) }; M (r, j)
R = { O, (i = e, j) }, R – правый репер, М (x, y)
Построенная таким образом ДПСК называется согласованной с полярной или присоединенной к полярной СК
М = О Ç ММ ^ О
x = | OM |;y = | M M | (1)
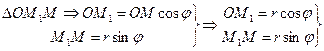 (2)
(2)
(1), (2) Þ 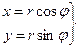 (3) – формула перехода полярной СК присоединенной к ДПСК.
(3) – формула перехода полярной СК присоединенной к ДПСК.
Решая систему (3) относительно r и j получим формулы обратного перехода
x + y = r (cos j + sin j)
r = 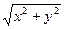
r = 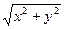 , cos j =
, cos j = 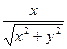 , sin j =
, sin j = 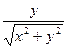 ; tg j =
; tg j = 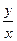 (4)
(4)
В качестве примера использования формул перехода от полярной системы, присоединенной к ДПСК решим задачу на вычисление расстояния между точками.
Задача № 5
P = (O, (e) } R = { O, (i = e, j) } – присоед. ДПСК
M (r, j) M (x, y); M (x, y)
M (r, j) d = 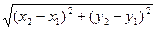
d = | M, M | Используя формулы (3)
d = 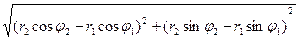
Найти d -? Раскрывая скобки и приводя подобные:
D = 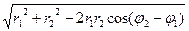
Лекция № 8
Геометрическое истолкование уравнений и неравенств между координатами. Алгебраическая линия и ее порядок.
Пусть F (x, y) – математическое выражение, составленное из букв x, y. F (x, y) – “терм”
R = { O, (e, e) }
Тогда введя на плоскости афинную СК, мы можем при помощи этого выражения определить следующие 6 фигур:
Ф = { M (x, y) | F (x, y) = 0 } Очевидно, что между ними существуют
Ф = { M (x, y) | F (x, y) > 0 } следующие зависимости:
Ф = { M (x, y) | F (x, y) < 0 } Ф = Ф 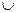 Ф
Ф
Ф = { M (x, y) | F (x, y) ³ 0 } Ф = Ф 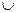 Ф
Ф
Ф = { M (x, y) | F (x, y) 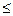 0 } Ф = Ф
0 } Ф = Ф 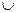 Ф
Ф
Ф = { M (x, y) | F (x, y) ¹ 0 }
Пример: F (x, y) = y; R = {O, (e, e) }
Ф = { M {x, y) | y = 0 } = 0
Ф = { M y (x, y) | y > 0 } = L (верхняя полуплоскость)
Ф = { M {x, y) | y < 0 } = L (нижняя полуплоскость)
Ф = { M {x, y) | y ³ 0 } = O 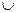 L
L
Ф = { M {x, y) | y 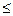 0 } = O
0 } = O 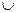 L
L
Ф = { M {x, y) | y ¹ 0 } = L 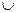 L
L
При изучении геометрии аналитическими методами обычно возникают 3 взаимообратные задачи.
Задача 1: В данной афинной СК фигура задана своими уравнениями или неравенствами. Требуется изучить эту фигуру и изобразить ее геометрические свойства.
Задача 2: Задана некая геометрическая фигура на плоскости, как множество точек, каждая из которых обладает определенными характерными свойствами. Требуется относительно АСК написать ее уравнение или неравенство.
Примером задачи 1-го типа является пример, рассмотренный выше. Приведем пример задачи второго типа.
Дата публикования: 2015-07-22; Прочитано: 372 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
