 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры проверки статистических гипотез
|
|
Ниже приводятся три примера проверки статистических гипотез. Необходимо строго придерживаться конкретных условий, которые даны, и формул, по которым проводится проверка. Гипотезы таковы: 1) гипотеза о равенстве средних величин при известных дисперсиях (большие независимые выборки); 2) гипотеза о равенстве дисперсий двух выборок (малые выборки); 3) гипотеза о равенстве двух выборочных долей (большие выборки).
Этапы работы:
- Выдвигаются нулевая и конкурирующая гипотезы, а также определяется, односторонняя или двусторонняя проверка будет применяться.
- Определяется ошибка I рода a (чаще всего от 1 до 10%) и в зависимости от характера проверки фиксируется критическая точка Т кр. (Например, при вероятности a = 0,05 при односторонней проверке Т кр = 1,65, а при двусторонней Т кр = 1,96) (таблица интеграла вероятностей).
- Рассчитываются фактические значения критерия Т ф.
- Сравниваются Т ф и Т кр. и затем делается вывод. Возможны 3 ситуации:
а) Т ф > Т кр: Н 0 отклоняется;
б) Т ф < Т кр: Н 0 принимается;
в) Т ф.» Т кр., необходимо продолжить исследование на другом материале и (или) увеличить объем выборки.
Пример 7.4. В двух случайных выборках работников численностью n 1 = 27 и n 2 = 33 средняя выработка за смену составляет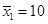 
, 
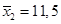единиц соответственно при дисперсиях 
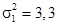и 
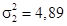. Можно ли считать такое расхождение случайным или же оно является следствием различных условий организации труда?
Решение
Ошибку I рода a принимаем на уровне 5%. Нулевая гипотеза Н 0: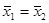 
; альтернативная Н 1: 
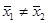, т.е. либо 
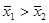, либо 
.
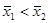Выписываем формулу критической статистики и находим фактическое значение Т ф:
.
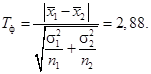Приняв уровень значимости a = 5%, мы тем самым определили критическую точку, разделяющую область принятия Н 0 от области ее отклонения. По таблице интеграла вероятностей и при доверительной вероятности 1 – 0,05 = 0,95 находим Т кр = 1,96. Т ф > Т кр, т.е. Т ф = 2,88 попадает в критическую зону, отклоняя тем самым нулевую гипотезу. Сам факт отклонения гипотезы Н 0 не означает, что она является ложной. Напомним, что принятый нами уровень 5%, или 0,05, означает, что в 5 случаях из 100 мы рискуем допустить a, т.е. отвергнуть верную гипотезу (рис. 7.1 и 7.2).
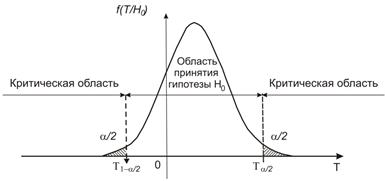
Рис. 7.1 [xl]
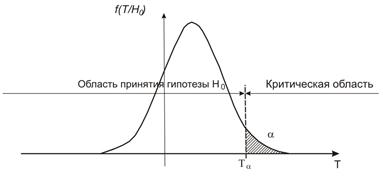
Рис. 7.2
Пример 7.5. Известны объемы и выборочные исправленные дисперсии двух выборок: n 1 = 9; s 2 = 1,4 и n 2 = 12; s 2 = 4,7. На уровне значимости 0,05 необходимо проверить гипотезу Н 0: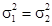 
против конкурирующей гипотезы H 1: 
.
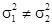Решение
Проверяем гипотезу Н 0: 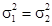генеральной совокупности.
Рассчитываем фактические значения критерия F Фишера — Снедекора (бóльшая дисперсия всегда в числителе) и получаем
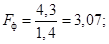
Из таблицы критических точек F -распределения Фишера (табл. П2.13) находим F кр = 3,31. При a = 0,05 F кр. > F ф. Вывод: нет основания отклонить Н 0 о равенстве дисперсий, различия между дисперсиями несущественные, случайные.
Пример 7.6. Проводились клинические испытания нового лекарства. В выборке участвовало 830 мужчин и 945 женщин. У 36 мужчин и 60 женщин наблюдались неблагоприятные побочные явления. Можно ли утверждать, что у женщин побочные явления возникают чаще?
Решение
Введем обозначения: n м = 830; n ж = 945.
Доля (%) мужчин с побочными явлениями p м = 36/830 = 0,0433 (4,33%); доля (%) женщин с побочными явлениями p ж = 65/945 = 0,0688 (6,88%).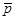 
— средняя доля мужчин и женщин, имеющих побочные явления: 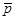= (36 + 60)/1775 = 0,054; 
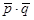= 0,051. Статистика имеет следующий вид:
Уровень значимости 0,03 (3%), проверка двусторонняя.
Подставляем в формулу полученные значения и получаем Т ф = 2,32. Учитывая выбранный нами уровень значимости 0,03, по таблице интеграла вероятности находим 1 – 0,03 = 0,97, Т кр = 2,17.
Вывод: Т ф. превышает Т кр и попадает в критическую зону (правее точки 2,17), тем самым отвергая Н 0: p м = pж. Мы принимаем конкурирующую Н 1: p м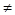 
p ж, т.е. мы вправе сделать вывод, что лекарство действует по-разному на мужчин и женщин и что различие не является случайным, такой вывод сделан с вероятностью 0,97.
Заметим, кстати, что если бы мы сформулировали Н 1: p ж > p м, то вывод был бы тем же самым. При 3%-ном уровне значимости Т кр.при односторонней проверке равно 1,89. Двусторонняя проверка более «строгая», нежели односторонняя. Рубеж 2,17 преодолеть труднее, чем 1,89. Будет ли проведена односторонняя или двусторонняя проверка — решается по смыслу самой задачи, т.е. нас интересует факт различия в обе стороны или только в одну.
В заключение приведем пример ситуации, когда Н 0 нельзя отклонить.
Пример. 7.7. По многолетним данным средний проходной балл составлял 50 с дисперсией 151,3. Многие эксперты считали, что величина балла несколько занижена (что ведет к набору слабо подготовленных школьников) и предлагали поднять планку до 54. Для проверки этого предположения была произведена случайная выборка n = 30 школьников, которые набрали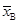 
= 54. Необходимо проверить, существенно ли различие 
= 50 и 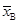= 54 при уровне значимости a = 0,02 (2%), правосторонняя проверка; Н 0: 
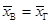; Н 1: 
:
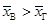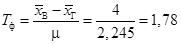; Т кр = 2,06.
Вывод: Н 0 отклонить не удалось. Проходной балл остается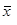 
= 50. А что если на самом деле верна Н 1: = 54, т.е. школьники теперь лучше подготовлены? Если это так, то, принимая Н 0, мы допускаем ошибку II рода b (вероятность принять неверную гипотезу). Ошибку b и мощность критерия М = 1 – b можно посчитать по-разному. В нашем случае М = 0,5 — Ф(2,06 – 1,78) = 0,5 – Ф(0,28) = 0,39; b = 0,61. 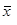Это вероятность того, что не будет ошибочно принята ложная гипотеза Н 0: = 50.
При одновременном фиксировании a и b до проведения выборочного исследования необходимо определить требуемый объем выборки, что может быть сделано применением к нашим условиям (a = 0,02; b = 0,61; n = 30). Если бы мы приняли a = 0,02, b = 0,1, то[xli]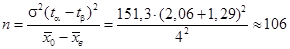 
, т.е. объем выборки следовало бы увеличить в 3,5 раза.
Дата публикования: 2014-10-20; Прочитано: 1509 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
