при каждом сочетании уровней факторов

№	x 0	x 1	x 2	x 3	y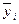
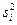
	+1	–1	–1	–1	y 11, y 12, …, y 1 m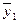
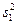
	+1	+1	–1	–1	y 21 y 22, …, y 2 m
	+1	–1	+1	–1	y 31, y 32, …, y 3 m
	+1	+1	+1	–1	y 41, y 42, …, y 4 m
	+1	–1	–1	+1	y 51, y 52, …, y 5 m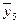
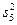
	+1	+1	–1	+1	y 61, y 62, …, y 6 m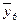
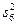
	+1	–1	+1	+1	y 71, y 72, …, y 7 m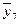
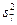
	+1	+1	+1	+1	y 81, y 82, …, y 8 m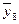

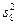
Однородность дисперсий проверяется по критерию Кохрена. Отношение максимальной дисперсии к сумме всех дисперсий

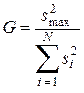(11.12)

сравнивается с табличным значением G _{1- p} ( f ₁, f ₂) для р = 0,05 и чисел степеней свободы f ₁ = m – 1 и f ₂ = N. Если G £ G _{1- p} ( f ₁, f ₂), то выборочные дисперсии однородны. Тогда наилучшей оценкой дисперсии воспроизводимости будет средневзвешенная дисперсия

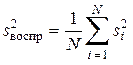(11.13)

с числом степеней свободы f _воспр = N (m – 1).

Коэффициенты уравнения регрессии определяются по формуле

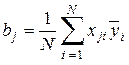. (11.14)

Поскольку дисперсия среднего в m раз меньше дисперсии единичного измерения, т. е.

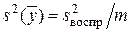, (11.15)

то выборочные среднеквадратичные отклонения коэффициентов рассчитываются следующим образом:

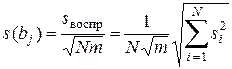. (11.16)

Значимость коэффициентов проверяется по критерию Стъюдента: если

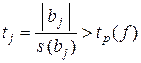, (11.17)

где t_p (f ) — табличное значение критерия Стъюдента для р = 0,05 и числа степеней свободы f = N (m – 1), то коэффициент значимо отличается от нуля.

Адекватность уравнения регрессии эксперименту проверяется по критерию Фишера. Дисперсия адекватности равна

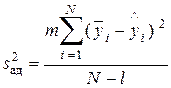, (11.18)

где l — число значимых коэффициентов в уравнении регрессии.

Уравнение адекватно эксперименту, если

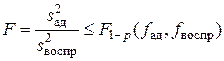, (11.19)

где F _{1- p} (f _ад, f _воспр) — табличное значение критерия Фишера для р = 0,05 и чисел степеней свободы f _ад = N – l и f _воспр = N (m – 1). В противном случае для описания результатов эксперимента необходимо увеличить порядок аппроксимирующего полинома.

11.3. Дробный факторный эксперимент. Планы типа 2 ^{k -1}

Число необходимых опытов в условиях линейной модели существенно сокращается при проведении дробных факторных экспериментов (дробных реплик от ПФЭ). В качестве реплики обычно используется полный факторный эксперимент для меньшего числа факторов. При этом вычисление коэффициентов уравнения и оценка их значимости проводится так же, как и в рассмотренных выше примерах ПФЭ 2² и 2³. Число опытов в дробной реплике должно быть больше или равно числу неизвестных коэффициентов в уравнении регрессии.

Спланируем дробный факторный эксперимент для получения линейного уравнения регрессии небольшого участка поверхности отклика при трех независимых факторах:

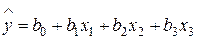. (11.20)

Постановка ПФЭ 2³ требует проведения 8 опытов. Для решения же поставленной задачи можно ограничиться 4 опытами, если в матрице планирования ПФЭ 2² (табл. 10, лекция 10) использовать столбец х ₁ х ₂ в качестве плана для х ₃. Матрица планирования такого сокращенного эксперимента — ДФЭ типа 2^3-1, или полуреплики от ПФЭ 2³, — представлена в табл. 14.

Таблица 14

Матрица планирования ДФЭ типа 2^3-1

№ опыта	х 0	х 1	х 2	х 3	y
	+1	–1	–1	+1	y 1
	+1	–1	+1	–1	y 2
	+1	+1	–1	–1	y 3
	+1	+1	+1	+1	y 4

Проведение ДФЭ по предложенной схеме позволяет оценить свободный член и три коэффициента при линейных членах уравнения (11.20), однако при этом они будут являться несмешанными оценками теоретических коэффициентов только в том случае, если генеральные коэффициенты регрессии при парных взаимодействиях равны нулю. В противном случае найденные выборочные коэффициенты будут смешанными оценками теоретических:

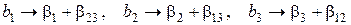. (11.21)

Генеральные коэффициенты не могут быть оценены по отдельности на основании только 4 опытов, поскольку при этом столбцы для линейных членов и парных произведений одинаковы (например, элементы вычисленного столбца для произведения х ₂ х ₃ в точности совпадут с элементами столбца х ₁). Чтобы определить, оценкой суммы каких именно генеральных коэффициентов явяются выборочные коэффициенты, удобно пользоваться генерирующим соотношением

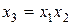, (11.22)

в общем случае означающим, какой именно столбец ПФЭ 2 ^k был использован в качестве плана для введения (k + 1)-го фактора в ДФЭ. При умножении обоих частей (11.22) на x ₃, получаем

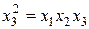. (11.23)

Единичный столбец

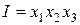(11.24)

называется определяющим контрастом и позволяет определить, элементы каких столбцов в расширенной матрице планирования одинаковы. Умножая I по очереди на x ₁, x ₂ и x ₃, получаем

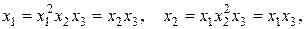
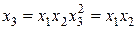, (11.25)

в точности соответствующих системе смешанных оценок (11.21).

При постановке ДФЭ с числом факторов k ³ 4 в зависимости от генерирующего соотношения выборочные коэффициенты регрессии оказываются смешанными оценками того или иного сочетания генеральных коэффициентов. Поэтому важно заранее определиться с тем, какая информация является наиболее важной в данном исследовании, и в зависимости от поставленной задачи подобрать нужную дробную реплику.

Рассмотрим, например, планирование ДФЭ типа 2^4‑1, представляющего собой полуреплику от ПФЭ 2⁴. В качестве реплики используем ПФЭ 2³ (табл. 12). Используем два генерирующих соотношения:

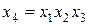, (11.26)

. (11.27)

Для соотношения (11.26) определяющим контрастом будет

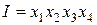. (11.28)

Тогда

;

;

;

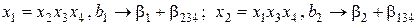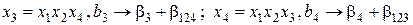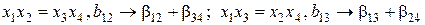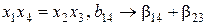. (11.29)

В реальных задачах влияние тройных взаимодействий обычно равно нулю. Следовательно, генерирующее соотношение (11.26) следует использовать, если наибольший интерес представляют оценки для линейных эффектов.

Для соотношения (11.27) определяющим контрастом будет

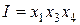. (11.30)

Тогда

;

;

;

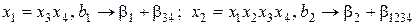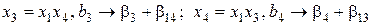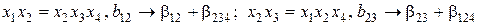. (11.31)

Следовательно, дробную реплику с генерирующим соотношением x ₄ = x ₁ x ₃ следует использовать, если наибольший интерес представляют эффекты парных взаимодействий.

В общем случае число опытов в дробной реплике должно удовлетворять следующему соотношению:

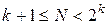, (11.32)

где k — число факторов. Если число опытов равно числу определяемых коэффициентов в линейном уравнении регрессии (N = k + 1), дробная реплика представляет собой линейный насыщенный план, для которого все линейные эффекты смешаны с эффектами взаимодействия. Число степеней свободы остаточной дисперсии в таких планах равно нулю, поэтому для проверки адекватности линейного уравнения необходимо проведение дополнительных опытов.

Итак, рассмотренные двухуровневые планы ПФЭ 2 ^k и ДФЭ 2 ^{k -1} обладают следующими свойствами: вычисления просты; все коэффициенты регрессии определяются независимо друг от друга и с одинаковой и минимальной дисперсией; каждый коэффициент рассчитывается по результатам всех опытов.

ЛЕКЦИЯ 12

Оптимизация методом крутого восхождения по поверхности отклика. Описание функции отклика в области, близкой к экстремуму. Композиционные планы Бокса-Уилсона. Ортогональные планы второго порядка, расчет коэффицентов уравнения регрессии. Метод последовательного симплекс-планирования.

12.1. Оптимизация методом крутого восхождения

по поверхности отклика

Задача оптимизации сводится к опытному определению такого сочетания уровней k факторов (координаты точки в (k +1)-мерном факторном пространстве), при котором достигается максимальное (минимальное) значение выходного параметра y (или нескольких параметров), т. е. функция отклика системы

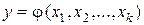
принимает экстремальное значение.

Рассмотрим случай, когда на систему оказывают влияние только два фактора (х ₁ и х ₂ в безразмерном масштабе). Построим контурные сечения y = const поверхности отклика при k = 2 (рис. 3 а).

Рис. 3. Движение по поверхности отклика (а) к экстремуму

в традиционном эксперименте и в методе крутого восхождения (б)

Поиск экстремальной точки поверхности отклика в традиционном эксперименте проводится следующим образом. В точке L с известным значением у фиксируется один из факторов, например х ₁, и начинается движение из этой точки вдоль оси х ₂. Движение по х ₂ продолжается до тех пор, пока не прекращается прирост y (рис. 3 б). В точке М с наилучшим значением выходного параметра фиксируется фактор х ₂ и начинается движение в направлении оси х ₁. В точке N со следующим наилучшим значением y снова фиксируется х ₁ и начинается движение по х ₂ и т. д. Очевидно, что путь к экстремуму по ломаной кривой LMNR (рис. 3 б) не является оптимальным.

Кратчайшим, наиболее крутым путем достижения экстремума будет движение из точки L по градиенту перпендикулярно изолиниям y = const (на рис. 3 б этот путь показан пунктирной линией). Для рассматриваемого случая градиент функции отклика равен

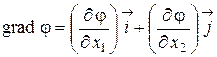, (12.1)

где 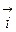и 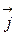— орты координатных осей. Предполагается, что функция j непрерывна, дифференцируема и не имеет особых точек.

Для реализации метода крутого восхождения Бокс и Уилсон предложили шаговый метод движения по поверхности отклика. В окрестности точки L ставится эксперимент для локального описания поверхности отклика линейным уравнением регрессии:

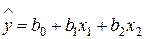. (12.2)

Движение из точки L начинается в направлении градиента линейного приближения

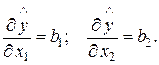(12.3)

Для случая, представленного на рис. 3 б, выборочные коэффициенты при линейных членах в окрестности точки L имеют разные знаки: b ₁ > 0, b ₂ < 0, поэтому при движении к максимуму функции отклика значение х ₁ увеличивается, а х ₂ уменьшается. Движение по градиенту линейного приближения продолжается до тех пор, пока не прекращается прирост y. В точке с наибольшим значением y (центр плана) ставится новая серия опытов и определяется новое направление движения по поверхности отклика. Такой шаговый процесс продолжается до достижения области, близкой к экстремуму.

При постановке опытов величина шага должна быть пропорциональна произведению коэффициента на интервал варьирования: b_j D z_j. Например, при движении из точки L следующий эксперимент ставится в точке со значениями x ₁ и х ₂, отличающимися от начальных на величины 2 b ₁D z ₁ и 2 b ₂D z ₂ соответственно. В общем случае направление градиента будет зависеть от выбранного интервала варьирования независимых факторов. При изменении в n раз интервала варьирования некоторого j -фактора величина шага для него меняется в n ² раз, так как при этом в n раз изменяется и коэффициент регрессии b_j. Инвариантными к изменению интервала остаются только знаки составляющих градиента. При увеличении числа рассматриваемых факторов более двух оптимизация методом крутого восхождения по поверхности отклика проводится аналогичным способом.

12.2. Описание функции отклика в области, близкой

к экстремуму. Композиционные планы Бокса-Уилсона

В области, близкой к экстремуму, (или «почти стационарной области») функция отклика существенно нелинейна, поэтому для ее адекватного описания необходимо использовать нелинейные полиномы. В настоящее время для этой цели наиболее широко применяют полиномы второго порядка, для получения которых имеются хорошо разработанные планы эксперимента.

Для описания полиномом второго порядка эксперимента, реализованного для нахождения оптимальных условий процесса, число опытов N в плане должно быть не меньше числа определяемых коэффициентов в уравнении регрессии второго порядка для k факторов

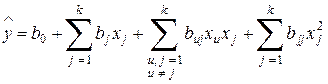. (12.4)

Выборочные коэффициенты (12.4) являются оценками соответствующих коэффициентов уравнения теоретической регрессии:

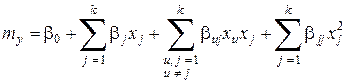. (12.5)

В зависимости от числа рассматриваемых факторов число коэффициентов l уравнения регрессии (12.4) определяется по формуле

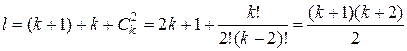, (12.6)

где 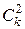— количество сочетаний из k факторов по два, равное числу эффектов парного взаимодействия.

В области, близкой к экстремуму, становятся значимыми эффекты парного взаимодействия и квадратичные эффекты. Поэтому то, что адекватное описание результатов эксперимента требует использования полиномов второго порядка, может служить признаком нахождения в почти стационарной области. Близость к этой области можно также установить, поставив дополнительно к ПФЭ 2 ^k или ДФЭ 2 ^{k -1} серию опытов в центре плана. Среднее значение результатов этих опытов является оценкой для свободного члена уравнения (12.5):

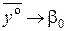. (12.7)

Выборочный коэффицент b ₀, вычисляемый по формуле

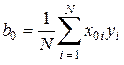, (12.8)

оценивает сумму свободного и квадратичных членов:

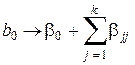. (12.9)

Поэтому, чем больше разность

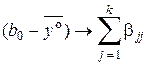, (12.10)

тем значимее квадратичные эффекты.

Для описания поверхности отклика полиномами второго порядка независимые факторы в планах должны принимать не менее трех разных значений. Эксперимент, в котором каждый из k факторов рассматривается на трех уровнях и реализуются все возможные сочетания уровней факторов, является ПФЭ типа 3 ^k. В качестве примера в табл. 15 представлена матрица планирования ПФЭ 3².

Проведение ПФЭ 3 ^k требует большого числа опытов, намного превышающего число определяемых коэффициентов l в уравнении (12.4) уже при k > 2:

k
3 k
l

Таблица 15

Матрица планирования ПФЭ 3²

№ опыта	х 1	х 2	y
	–1	–1	y 1
		–1	y 2
	+1	–1	y 3
	–1		y 4
			y 5
	+1		y 6
	–1	+1	y 7
		+1	y 8
	+1	+1	y 9

Сократить общее число опытов при условии получения несмешанных оценок для линейных эффектов и эффектов взаимодействия можно с помощью композиционных планов Бокса-Уилсона. Ядро таких планов при k < 5 составляет ПФЭ 2 ^k, и полуреплика от него при k ³ 5.

Если линейное уравнение регрессии оказалось неадекватным эксперименту, необходимо:

1) добавить 2 k звездных точек, расположенных на координатных осях факторного пространства. Координаты звездных точек в общем случае равны

,

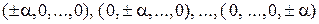где a — расстояние от центра плана до звездной точки, или звездное плечо;

2) увеличить число экспериментов в центре плана n ₀.

Общее число опытов в матрице композиционного плана при k £ 4 составляет

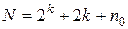. (12.11)

Рассмотрим построение композиционных планов на примере k = 2 (рис. 4). Точки 1, 2, 3, 4 образуют ПФЭ 2², точки 5, 6, 7, 8 являются звездными точками с координатам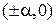и и 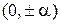, координаты n ₀ опытов в центре плана нулевые — (0, 0).

Композиционный план второго порядка для двух факторов представлен в табл. 16, при этом в центре плана выполнена серия из трех опытов (№ 9–11).

Рис. 4. Композиционный план второго

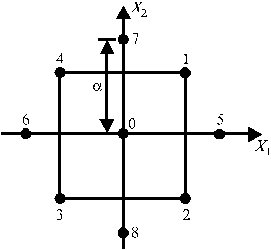порядка для двух факторов

Таблица 16

Композиционный план второго порядка для двух факторов

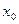
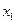
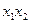
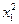
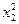
№ опыта							y
	+1	+1	+1	+1	+1	+1	y 1
	+1	+1	–1	–1	+1	+1	y 2
	+1	–1	–1	+1	+1	+1	y 3
	+1	–1	+1	–1	+1	+1	y 4
	+1	+a			a2		y 5
	+1	–a			a2		y 6
	+1		+a			a2	y 7
	+1		–a			a2	y 8
	+1						y 9
	+1						y 10
	+1						y 11

12.3. Ортогональные планы второго порядка,

расчет коэффицентов уравнения регрессии

Выбор звездного плеча в композиционных планах Бокса–Уилсона может быть произвольным, однако расчеты коэффициентов уравнения регрессии при k < 5 существенно упрощаются, если величина плеча определяется исходя из следующего уравнения:

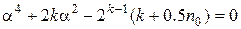. (12.12)

Значения a², определенные по (12.12), приведены в табл. 17.

Таблица 17

Значения a² для k факторов и n ₀ опытов в центре плана

n 0	k		n 0	k
	1.00	1.476	2.00			1.742	2.325	2.950
	1.160	1.650	2.164			1.873	2.481	3.140
	1.317	1.831	2.390			2.00	2.633	3.310
	1.475	2.00	2.580			2.113	2.782	3.490
	1.606	2.164	2.770			2.243	2.928	3.66

Выбрав a, проведем следующее линейное преобразование квадратичных столбцов:

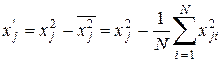. (12.13)

Композиционные планы, полученные таким образом, называются ортогональными планами второго порядка.

Ортогональный план второго порядка при k = 2 и n ₀ = 1 представлен в табл. 18. За его основу взят композиционный план для двух факторов (табл. 16) с общим числом опытов N = 9. Величину звездного плеча определим по табл. 17: a² = 1, a = 1. Средние значения элементов квадратичных столбцов в табл. 16 равны

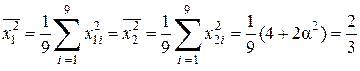. (12.14)

В математической статистике доказывается, что для ортогональных планов второго порядка все коэффициенты уравнения регрессии определяются независимо друг от друга по формуле

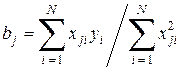, (12.15)

а дисперсии коэффициентов равны

. (12.16)

Таблица 18

Ортогональный план второго порядка для двух факторов

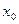
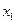
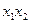
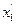
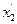
№ опыта							y
	+1	+1	+1	+1	+1/3	+1/3	y 1
	+1	+1	–1	–1	+1/3	+1/3	y 2
	+1	–1	–1	+1	+1/3	+1/3	y 3
	+1	–1	+1	–1	+1/3	+1/3	y 4
	+1	+a			+1/3	–2/3	y 5
	+1	–a			+1/3	–2/3	y 6
	+1		+a		–2/3	+1/3	y 7
	+1		–a		–2/3	+1/3	y 8
	+1				–2/3	–2/3	y 9

Для определения дисперсии воспроизводимости необходимо выполнить серию опытов в центре плана. В результате расчетов по матрице с преобразованными столбцами для квадратичных эффектов (табл. 18) получаем следующее уравнение:

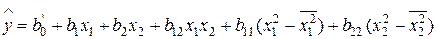. (12.17)

Чтобы перейти к обычной записи уравнения регрессии в виде

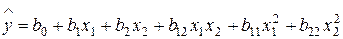, (12.18)

определим b ₀ по формуле

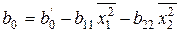(12.19)

с дисперсией, равной

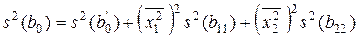. (12.20)

Значимость коэффициентов проверяется по критерию Стъюдента. Если

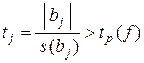, (12.21)

где t_p (f ) — табличное значение критерия Стъюдента для р = 0,05 и числа степеней свободы дисперсии воспроизводимости, то коэффициент значимо отличается от нуля.

Коэффициенты уравнения регрессии, получаемые при помощи ортогональных планов второго порядка, определяются с разной точностью. В случае, когда k £ 4, согласно (12.16) имеем

;

;

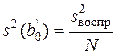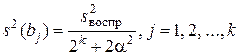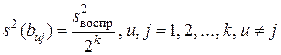; (12.22)

.

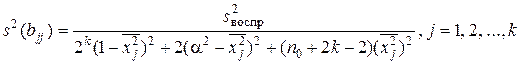После исключения незначимых коэффициентов проводится проверка адекватности уравнения по критерию Фишера. Уравнение адекватно эксперименту, если

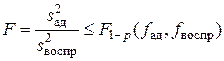, (12.23)

где F _{1- p} (f _ад, f _воспр) — критерий Фишера для р = 0,05; f _ад = N – l — число степеней свободы дисперсии адекватности (l — число значимых коэффициентов в уравнении регрессии); f _воспр — число степеней свободы дисперсии воспроизводимости.

12.4. Метод последовательного симплекс-планирования

В рассмотренных выше планах ПФЭ 2² и 2³ экспериментальные точки располагались в вершинах квадрата и куба соответственно. В качестве экспериментального плана можно также использовать регулярный симплекс. Симплексом в k -мерном пространстве называют выпуклый многогранник, имеющий ровно (k + 1) вершину, каждая из которых определяется пересечением k гиперплоскостей данного пространства. Симплекс называется регулярным, если расстояния между всеми его вершинами равны. Примерами регулярных симплексов являются правильный треугольник в двумерном пространстве и тетраэдр в трехмерном.

На практике планирование эксперимента с использованием регулярных симплексов применяется для решения задач оптимизации при движении к почти стационарной области. Для получения регулярного симплекса проводится линейное преобразование уровней факторов

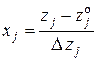, (12.24)

где 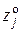— j -я координата центра плана; — интервал варьирования по j -фактору.

Оптимизация методом последовательного симплекс-планирования проводится следующим образом: исходная серия опытов планируется так, чтобы экспериментальные точки образовывали регулярный симплекс в факторном пространстве. После проведения опытов определяется вершина симплекса, соответствующая наихудшим результатам. Далее строится новый симплекс, для чего наихудшая точка исходного симплекса заменяется новой, расположенной симметрично относительно центра грани симплекса, находящейся против наихудшей точки. Новая точка вместе с оставшимися точками образует новый симплекс, центр тяжести которого смещен в сторону повышения качества процесса. После реализации опыта в дополнительной точке опять проводится выявление наихудшей вершины симплекса и т. д. При достижении области оптимума, симплекс начинает вращение вокруг вершины с максимальным значением отклика.

На рис. 5 показаны схемы достижения экстремума поверхности отклика методами крутого восхождения и симплекс-планирования на примере зависимости целевой функции y от двух факторов. При оптимизации методом крутого восхождения (рис. 5 а) в окрестности точки М поставлен ПФЭ 2², движение по градиенту линейного приближения осуществлялось в опытах 5–9. Далее был поставлен новый ПФЭ 2² (точки 10–13) с центром в точке 7, в которой было получено наилучшее значение y. Движение по новому градиенту (точки 14–15) приводит к экстремуму.

При оптимизации методом симплекс-планирования (рис. 5 б) в исходном симплексе (точки 1–3) худшей точкой оказалась точка 2. Ее зеркальным отражением относительно с ₁ — центра грани 1–3 — является точка 4. В новом симплексе 1, 3, 4 худшей оказалась точка 1, в результате ее зеркального отражения получен симплекс 3, 4, 5 и т. д. Область оптимума достигается при реализации симплекса 9, 10, 11.

Хотя оба рассмотренных метода требуют проведения примерно одинакового числа опытов, симплекс-планирование имеет ряд важных

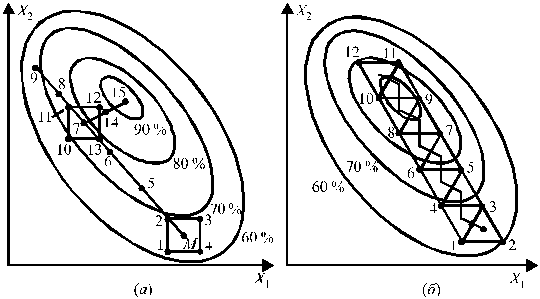Рис. 5. Достижение экстремума поверхности отклика

методами крутого восхождения (а) и симплекс-планирования (б)

преимуществ: при использовании этого метода параметр оптимизации y может измеряться приближенно, достаточно иметь возможность проранжировать его величину; можно одновременно учитывать несколько параметров оптимизации; метод не предъявляет жестких требований к локальной аппроксимации поверхности отклика уравнением регрессии.

На практике рекомендуется ориентировать исходный симплекс в факторном пространстве следующим образом: центр симплекса совпадает с началом координат, одна из вершин лежит на координатной оси, а остальные располагаются симметрично относительно координатных осей, плоскостей и гиперплоскостей (в многомерном случае). Тогда координаты вершин симплекса при k = 5 задаются матрицей

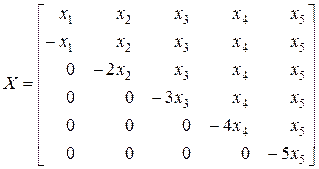. (12.25)

При k < 5 координаты вершин симплекса определяются частью матрицы (12.25), при этом число столбцов равно числу факторов, а число строк равно k + 1; при k > 5 для каждого добавленного фактора в матрицу (12.25) добавляются соответствующие столбец и строка. В общем случае число опытов в симплексной матрице для k независимых факторов N = (k + 1) равно числу коэффициентов линейного уравнения регрессии, т. е. симплексные планы являются насыщенными.

Если длину стороны симплекса принять равной 1, то

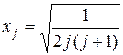. (12.26)

Для практического использования матрицы (12.25) ее числовые элементы заранее подсчитаны по формуле (12.26)

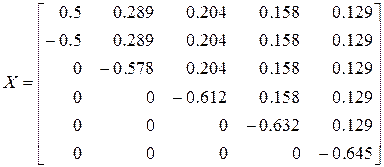. (12.27)

План эксперимента в безразмерном масштабе для k факторов состоит из k столбцов и k + 1 строки матрицы (12.27). Коэффициенты уравнения линейной регрессии

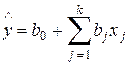(12.28)

вычисляются следующим образом:

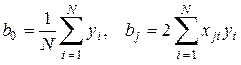. (12.29)

Если в одной из вершин симплекса поставить серию параллельных опытов и рассчитать дисперсию воспроизводимости, то выборочные дисперсии коэффициентов определяются по формуле

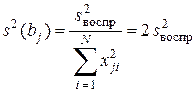. (12.30)

Следует отметить, что коэффициенты уравнения регрессии, полученные по симплексному плану, определяются с меньшей точностью по сравнению с коэффицентами, полученными при реализации ПФЭ 2 ^k и ДФЭ 2 ^{k -1}, для которых

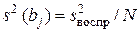. (12.31)

После реализации исходного симплекса требуется провести отражение наихудшей точки относительно центра противоположной грани. Координаты отраженной точки равны:

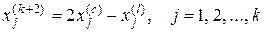, (12.32)

где 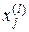— j -я координата наихудшей точки; 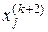— j -я координата новой точки, получаемой в результате отражения; 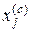— j -я координата центра противоположной грани, определяемая по формуле

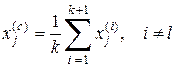, (12.33)

где 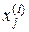— j -я координата i -й вершины симплекса (i = 1, 2, …, k +1).

Координаты центра оптимального симплекса (точка S) в почти стационарной области находятся следующим образом:

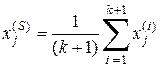. (12.34)

СОДЕРЖАНИЕ