Исходные данные для однофакторного дисперсионного анализа

Номер наблюдения	Уровни фактора А
а 1	а 2	…	аk
	y 11	y 21	…	yk 1
	y 12	y 22	…	yk 2
…	…	…	…	…
n			…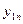
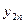
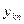
Итоги:	B 1, C 1	B 2, C 2	…	Bk, Ck

Предположим, что результат каждого опыта можно представить в виде следующей модели:

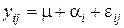, (9.1)

где m — суммарный эффект во всех опытах; a _i — эффект, обусловленный влиянием фактора А на i -уровне; e _ij — случайная ошибка опыта на i -уровне. Примем также, что наблюдения на фиксированном уровне фактора А нормально распределены относительно среднего значения (m + a _i) с общей дисперсией s²_ош.. Для того чтобы решить вопрос о значимости влияния фактора А, следует проверить нулевую гипотезу равенства математических ожиданий сумм (m + a _i) на различных уровнях этого фактора:

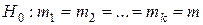, (9.2)

где m_i = M {m + a _i }.

Рассмотрим случай, когда на каждом уровне выполнено равное число опытов (n ₁ = n ₂ = … = n_k = n). Общее число опытов равно

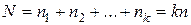. (9.3)

Обозначим сумму результатов всех опытов (итогов) на i -уровне через

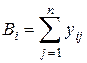, (9.4)

а сумму квадратов итогов на i -уровне через

. (9.5)

Тогда среднее значение наблюдений на i -уровне равно

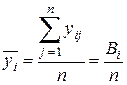, (9.6)

а общее среднее для всей выборки из N наблюдений —

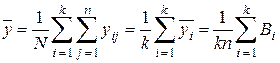. (9.7)

Общая выборочная дисперсия опытов определяется выражением

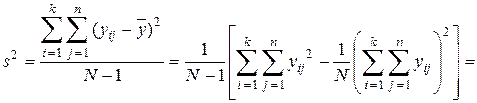
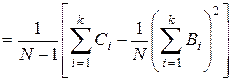, (9.8)

а выборочная дисперсия на i -уровне —

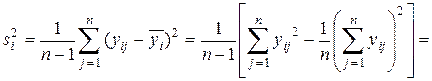
. (9.9)

Если выборочные дисперсии однородны (проверка по критерию Кохрена), то лучшей оценкой дисперсии s²_ош., характеризующей влияние случайных факторов, будет выборочная дисперсия

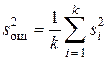(9.10)

с числом степеней свободы f _ош = k (n – 1) = N – k. Приближенно оценить дисперсию фактора А можно следующим образом:

. (9.11)

Для получения более точной оценки рассмотрим отклонение средних на фиксированных уровнях от общего среднего:

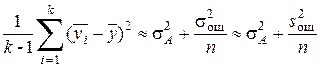. (9.12)

В данном случае под дисперсией фактора А понимают математическое ожидание среднего квадрата отклонений, обусловленного влиянием этого фактора. Выборочная дисперсия

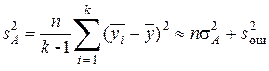(9.13)

с числом степеней свободы f_A = k – 1 используется для проверки нулевой гипотезы (9.2) по критерию Фишера.

При этом, если нулевая гипотеза (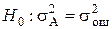) верна, выполняется следующее условие:

, (9.14)

т. е. различие между дисперсиям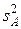и и 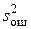является незначимым, и следовательно влияние фактора А на результаты опытов тоже незначимо (сопоставимо с эффектом случайности). При проверке гипотезы используется односторонний критерий, так как альтернативной гипотезой является 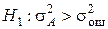. Если же

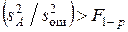, (9.15)

то нулевая гипотеза о равенстве математических ожиданий сумм (m + a _i) отвергается (влияние фактора А значимо). Чтобы выяснить, какие средние различны, можно использовать критерий Стъюдента, сравнивая средние попарно. Оценить влияние фактора А можно на основании (9.13):

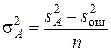. (9.16)

Если на каждом уровне выполнено разное число опытов, выборочная дисперсия фактора А рассчитывается по формуле

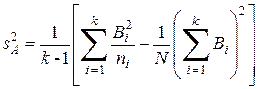, (9.17)

а выборочная дисперсия, характеризующая влияние случайных факторов, по формуле

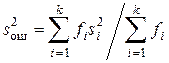, (9.18)

где f_i = n_i – 1. Число степеней свободы 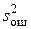равно f _ош = N – k.

Если дисперсия 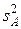значимо отличается от дисперсии 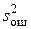, т. е. выполняется неравенство (9.15), то дисперсия фактора А оценивается по формуле

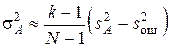. (9.19)

9.2. Двухфакторный дисперсионный анализ

Рассмотрим влияние на результаты опытов двух факторов А и В. Фактор А исследуется на k уровнях (i = 1, 2, …, k), фактор В — на m уровнях ( j = 1, 2, …, m). Пусть при каждом сочетании уровней факторов выполнено n параллельных опытов (q = 1, 2, …, n). Тогда общее число опытов равно N = nkm. Обозначим через y_ijq результат q ‑го опыта, выполненного на i -уровне фактора А и j -уровне фактора В.

Предположим, что результат каждого опыта можно представить следующим образом:

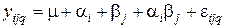, (9.20)

где m — общее среднее (суммарный эффект во всех опытах); a _i и b _j — эффекты, обусловленные влиянием фактора А на i -уровне и фактором В на j -уровне соответственно; e _ijq — случайная ошибка опыта, распределенная нормально с нулевым математическим ожиданием и дисперсией 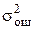; a _i b _j — эффект взаимодействия факторов. Величина a _i b _j характеризует отклонение среднего в (ij)-серии опытов от суммы первых трех членов в ур-и (9.20), а соответствующую ей дисперсию 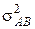можно оценить только при наличии параллельных опытов.

При отсутствии параллельных опытов (табл. 3) или в случае, если эффектом взаимодействия факторов пренебрегают, для описания результатов экспериментов используется линейная модель

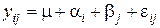. (9.21)

Таблица 3