 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Три правила знаходження первісної
|
|
|

|

|
«інтеграл еф від
позначається: 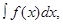 читається: ікс де ікс».
читається: ікс де ікс».
 - знак інтеграла,
- знак інтеграла, 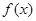 - підінтегральна функція,
- підінтегральна функція,
 підінтегральний вираз,
підінтегральний вираз,  змінна інтегрування.
змінна інтегрування.
|
пишуть: 
 Функція =>Загальний вид первісних Функція => Загальний вид первісних
Функція =>Загальний вид первісних Функція => Загальний вид первісних
 =>
=> 
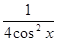 =>
=> 
 >
> 
 =>
=> 
 =>
=> 
 =>
=> 
 =>
=> 
 =>
=> 
 =>
=> 
 =>
=> 
Функція =>Загальний вид первісних
 =>
=> 
 =>
=> 
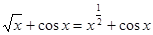 =>
=> 
 =>
=> 
 =>
=> 
 =>
=> 

 =>
=> 
Обчислити інтеграл: 
Розв’язання.
Представимо підінтегральний вираз у вигляді суми дробів, розділивши почленно чисельник на  . Застосуємо формулу інтеграла суми:
. Застосуємо формулу інтеграла суми:
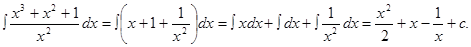
Знайти інтеграл: 
Розв’язання.
Представимо підінтегральний вираз у вигляді степеня з дробовим показником:

Знайти  якщо при
якщо при  первісна функції дорівнює 9.
первісна функції дорівнює 9.
Розв’язання.
Обчислимо інтеграл: 
Знайдемо сталу с: 


 Відповідь:
Відповідь: 







Обчислити площу фігури, обмеженої лініями: а) 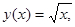


б) 

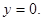
1. Будуємо задані лінії та штрихуванням відмічаємо фігуру, площу якої треба знайти. Встановимо, чи є ця фігура криволінійною трапецією:
2. Записуємо формулу для обчислення площі шуканої фігури:

3. Знаходимо межі інтегрування: а) 
б) 



4. Обчислюємо відповідні інтеграли.
Наприклад:
Обчислити площу фігури, обмеженої лініями: а) 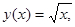

Будуємо задані лінії та штрихуванням відмічаємо фігуру, площу якої треба знайти.
Записуємо формулу для обчислення площі шуканої фігури:


Обчислити площу фігури, обмеженої лініями: а) 
Будуємо задані лінії та штрихуванням відмічаємо фігуру, площу якої треба знайти.
Записуємо формулу для обчислення площі шуканої фігури:


Обчислити площу фігури, обмеженої лініями: а) 

Будуємо задані лінії та штрихуванням відмічаємо фігуру, площу якої треба знайти. 
Записуємо формулу для обчислення площі шуканої фігури:

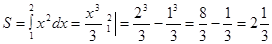
Дата публикования: 2014-11-18; Прочитано: 1289 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

 – первісна
для
– первісна
для 
 – первісна для
– первісна для 


 на цьому
проміжку.
на цьому
проміжку.
 одна
із первісних для
одна
із первісних для 