 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Другий тип задач
|
|
|
1) 9 пасажирів сідають в три вагони, знайти ймовірність:
А) що в кожний вагон зайде 3 пасажири;
Б) в один вагон зайде 4 пасажири, в 2-й 3 пасажири, в 3-й 2 пасажири;
В) в перший вагон зайде 4 пасажири,2-й 3 пасажири, 3-й 2 пасажири.
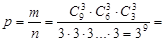
|







 А)
А)
…9 пасажирів мають 3 можливості тому 9 степінь
|



 Б)
Б)
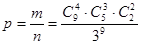
В чисельнику як говорить задача
В) 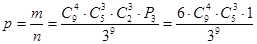
Доданки однакові тільки змінюється порядок множення тому рахуємо кількість.
2) У ліфт дев’ятиповерхового будинку зайшли 5-ть чоловік. Знайти ймовірність, що всі вийдуть на різних поверхах, якщо ймовірність вийти на всіх поверхах однакова.(8 тому що на першому зайшли)

|









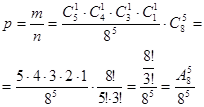 на
на 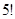 - скорочуемо
- скорочуемо
Треба порахувати скільки, порядок не цікавить тому комбінація
3)
|
 Знайти ймовірність, що дні народження 12-ти чоловік припадає на різні місяці.
Знайти ймовірність, що дні народження 12-ти чоловік припадає на різні місяці.












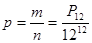
Р – перестановка
.
4) Знайти ймовірність, що принаймні ( складна подія ) 2 учні з групи народились в одному місяці. Якщо в групі:
А) 12чол;
Б) 11 чол;
В) 13 чол.
Всі в різних місяцях:
А) 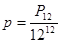 Б)
Б) 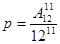 - схоже на 5 з 8. В)
- схоже на 5 з 8. В) 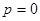 - не можна 13 в 12.
- не можна 13 в 12.
Якщо складна подія:
А) 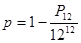 Б)
Б)  В)
В) 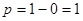
|
Події



 Сумісні. Не сумісні. Повна група. Рівно можливі.
Сумісні. Не сумісні. Повна група. Рівно можливі.

 Р=Р(А)+Р(В)-Р(АВ) протилежні
Р=Р(А)+Р(В)-Р(АВ) протилежні
 Простір елементарних подій
Простір елементарних подій
Незалежні Р=Р(А)Р(В) Залежні Р=Р(А)Р(ВА)
Протилежні Р=1-Р(А) Несумісні події Р=Р(А)+Р(В)
1) Ймовірність того що в бібліотеці можна відшукати довідник з алгебри 0,7, а з геометрії 0,8. Знайти ймовірність:
А) знайдеться тільки з алгебри;
Б) знайдуться обидва довідники;
В) знайдеться один довідник;
Г) знайдеться хоча б один довідник.
Характеристику даємо кожній складовій у всіх можливих проявах.
А – алгебра
Г – геометрія.
А) 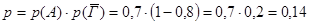
Б) 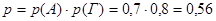
В) 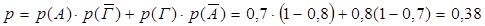
І спосіб
Г) 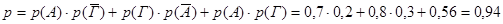
ІІ спосіб (протилежна подія не знайшли жоден)
Д) 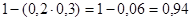
ІІІ спосіб Подія А і Г – сумісні
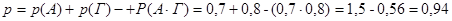
2) Олександр купив три різні акції, які можуть зростати в ціні, ймовірність того що 1-ша зросте – 0,7, друга – 0, 8, третя – 0,9. Знайти ймовірність:
А) всі зростуть в ціні;
Б) одна зросте в ціні;
В) дві зростуть;
Г) хоча б одна зросте в ціні.
3) З літер слова «Трансформатор» послідовно вибрати 5ть літер. Знайти ймовірність того, що ці літери в порядку їх вибору утворять «траса».
І спосіб. Залежні події
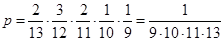 Знаменники зменшуються, бо попередні події відбулися
Знаменники зменшуються, бо попередні події відбулися
Т Р А С А чисельники вказують кількість літер в початковому слові
ІІ спосіб. Сукупність.(можна скласти схему)






 1
1 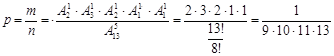
1 1 1
| Т2 | Р3 | А2 | Н1 | С1 | Ф1 | О2 | М1 |
5. Похідна та її застосування.
Основні вимоги до знань студентів.
· Розуміють значення поняття похідної для опису реальних процесів, зокрема механічного руху.
· Знаходять кутовий коефіцієнт і кут нахилу дотичної до графіка функції в даній точці.
· Знаходять швидкість змінення величини в точці;
· Наближено обчислюють значення і приріст функції в даній точці.
· Диференціюють функції, використовуючи таблицю похідних і правила диференціювання.
· Застосовують похідну для знаходження проміжків монотонності і екстремумів функції.
· Знаходять найбільше і найменше значення функції.
- Розв’язують нескладні прикладні задачі на знаходження найбільших і найменших значень реальних величин.

Розглянемо таблицю значень функції 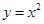
 в точках, які на числовій прямій розташовані досить близько до числа 2 (і в самій точці).
в точках, які на числовій прямій розташовані досить близько до числа 2 (і в самій точці).
Чим ближче аргумент 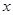 до числа 2 (пишуть
до числа 2 (пишуть 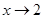 ), тим ближче значення функцій до числа
), тим ближче значення функцій до числа 
Записують так:

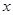
| 1,98 | 1,99 | 2,00 | 2,01 | 2,02 |

| 3,92 | 3,96 | 4,00 | 4,04 | 4,08 |
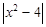
| 0,08 | 0,04 | 0,04 | 0,08 |
 Розглянемо таблицю значень функції
Розглянемо таблицю значень функції 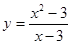 поблизу точки x = 3.
поблизу точки x = 3.
Якщо x→3 (x≠3), то ƒ(x) → 6:
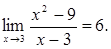
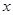
| 2,96 | 2,98 | 3,02 | 3,04 | |
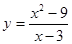
| 5,96 | 5,98 | не визначено | 6,02 | 6,04 |
| |ƒ(x) - 6| | 0,04 | 0,02 | 0,02 | 0,04 |
В загальному випадку 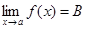 означає: якщо
означає: якщо 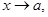 то
то 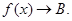

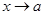
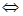
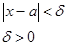 ; ƒ
; ƒ 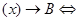
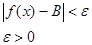
Число B називається границею функції f(x) при x, що прямує до a, якщо для будь-якого додатного числа ε знайдеться таке додатне число δ, що при всіх x ≠ a, які задовольняють нерівність |x-a|<δ, виконується нерівність: |ƒ(x)-B| < 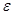
Якщо 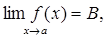 то B – єдина.
то B – єдина.

Теорія Практика
1. 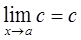
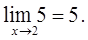
2. 
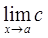 ƒ(x) =
ƒ(x) = 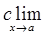 ƒ(x)
ƒ(x) 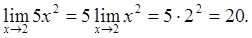
3. 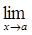 ( ƒ ( x)±ġ(x))=
( ƒ ( x)±ġ(x))= 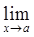 ƒ(x) ±
ƒ(x) ± 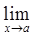 ġ(x)
ġ(x) 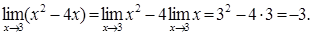
4. 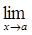 (ƒ(x)·ġ(x))=
(ƒ(x)·ġ(x))= 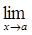 ƒ(x)·
ƒ(x)· 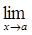 ġ(x)
ġ(x)
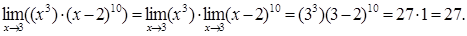
5. 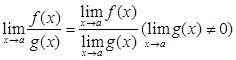

6. 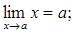
 якщо
якщо 


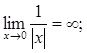 якщо
якщо  то
то 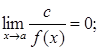


Функція 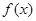
 називається неперервною в точці
називається неперервною в точці 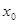 , якщо вона в ній визначена, границя функцій в точці
, якщо вона в ній визначена, границя функцій в точці 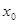 існує і дорівнює значенню функцій в цій точці.
існує і дорівнює значенню функцій в цій точці.
За цим означенням ставляться три вимоги:
1. функція повинна бути визначена в точці 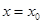 ;
;
2. функція 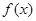 має границю в точці
має границю в точці 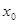 ;
;
3. 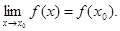
Наприклад: 
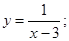
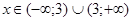

Дана функція не буде неперервною в точці 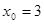 , оскільки вона не визначена при
, оскільки вона не визначена при 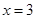 . Ті точки, в яких ці умови не виконуються, називаються точками розриву
. Ті точки, в яких ці умови не виконуються, називаються точками розриву 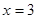 - точка розриву.
- точка розриву.
Дата публикования: 2014-11-18; Прочитано: 6140 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

