 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приложение определенного интеграла для вычисления площадей плоских фигур
|
|
Площадь S криволинейной трапеции, ограниченной непрерывной кривой 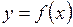 , двумя прямыми x = a и x = b и отрезком оси абсцисс
, двумя прямыми x = a и x = b и отрезком оси абсцисс 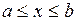 , вычисляется по одной из следующих формул:
, вычисляется по одной из следующих формул:
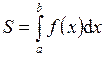 , если
, если 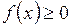 на отрезке
на отрезке 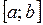 ;
;
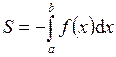 , если
, если 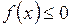 на отрезке
на отрезке 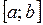 .
.
Площадь S фигуры, ограниченной двумя непрерывными кривыми  и
и 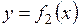 и двумя прямыми x = a и x = b, где
и двумя прямыми x = a и x = b, где 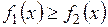 на отрезке
на отрезке 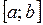 , вычисляется по формуле
, вычисляется по формуле
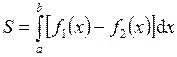 .
.
Рассмотрим примеры.
1. Вычислить площадь, ограниченную параболой 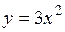 , прямыми x =2, x =4 и осью абсцисс.
, прямыми x =2, x =4 и осью абсцисс.
Площадь вычислим, используя формулу 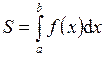 . Тогда
. Тогда
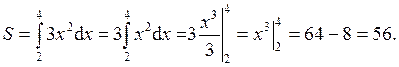
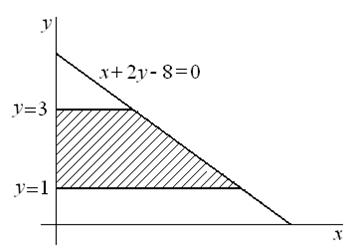
2. Вычислить площадь фигуры, ограниченной прямыми 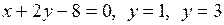 и осью ординат (рис.3).
и осью ординат (рис.3).
|
| Рис. 3 |
При вычислении искомой площади учтем, что изменены роли осей координат, т.е.:
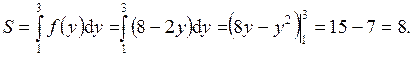
3. Вычислить площадь фигуры, ограниченной ветвью гиперболы 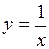 , прямыми x = -3, x = -1 и осью абсцисс.
, прямыми x = -3, x = -1 и осью абсцисс.
На отрезке 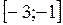 функция
функция 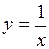 отрицательна. Поэтому для вычисления площади рассматриваемой фигуры воспользуемся формулой
отрицательна. Поэтому для вычисления площади рассматриваемой фигуры воспользуемся формулой
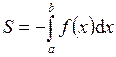 .
.
Получим
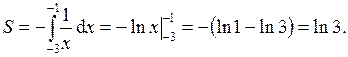
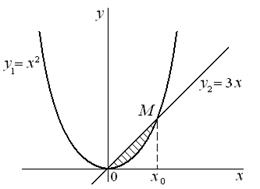
4. Вычислить площадь между линиями 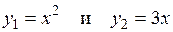 .
.
|
| Рис.4 |
Искомая площадь изображена на рис. 4 и представляет собой разность между площадью прямоугольного треугольника OMx 0 и площадью криволинейного треугольника, ограниченного сверху участком параболы:
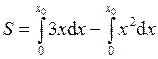 .
.
Абсциссу x 0 точки пересечения графиков находим, решая совместно уравнения 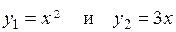 , откуда
, откуда  .
.
Подставляя полученное значение верхнего предела интегрирования, получаем
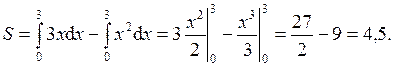
5.31 Вычислить площадь, ограниченную гиперболой 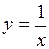 , осью абсцисс и ординатами
, осью абсцисс и ординатами 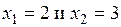 .
.
5.32 Вычислить площадь фигуры, заключенной между линиями 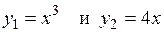 . Изобразить фигуру графически.
. Изобразить фигуру графически.
5.33 Найти площадь фигуры, заключенной между осью абсцисс и кривой 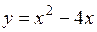 .
.
5.34 Найти площадь фигуры, ограниченной кривой 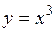 , прямыми
, прямыми 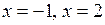 и осью абсцисс.
и осью абсцисс.
5.35 Вычислить площадь фигуры, образованной линиями 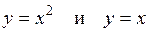 .
.
5.36 Определить площадь фигуры, ограниченной параболой 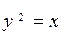 и прямой
и прямой 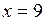 .
.
5.37 Найти площадь фигуры, заключенной между прямыми 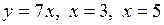 и осью абсцисс.
и осью абсцисс.
5.38 Вычислить площадь между линиями 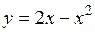 и
и  .
.
5.39 Определить площадь, ограниченную экспонентой 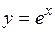 , осью абсцисс и ординатами
, осью абсцисс и ординатами 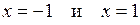 .
.
5.40 Найти площадь фигуры, ограниченной параболой  , осью абсцисс и прямыми
, осью абсцисс и прямыми 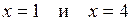 .
.
Дата публикования: 2014-11-18; Прочитано: 1646 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
