Непосредственное интегрирование

Функция 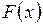называется первообразной для функции 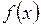, если

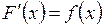
или

.

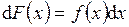Любая непрерывная функция 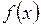имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым С.

Совокупность 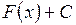всех первообразных для функции 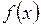называется неопределенным интегралом от этой функции.

Основные свойства неопределенного интеграла:

1.

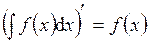
или

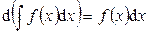
2.

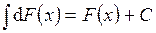
3.

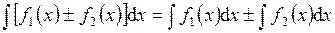
4.

Таблица простейших интегралов:
1.		7.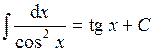
2.		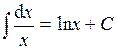8.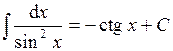
3.		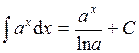9.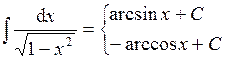
4.		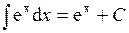10.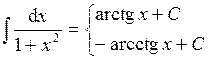
5.		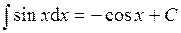11.
6.		12.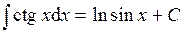

Проинтегрировать функцию 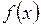- значит, найти её неопределенный интеграл. Непосредственное интегрирование основано на прямом использовании основных свойств неопределенного интеграла и таблицы простейших интегралов.

Рассмотрим следующие примеры:

1. Найти интеграл

.

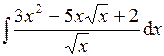Разделив почленно числитель на знаменатель, разложим подынтегральную функцию на слагаемые, после чего проинтегрируем каждое из полученных выражений:

Через С обозначен результат суммирования всех произвольных постоянных, получающихся при интегрировании каждого слагаемого.

2. Вычислить интеграл

Представим подынтегральную функцию следующим образом:

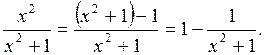
Тогда

3. Найти интеграл

Представим подынтегральную функцию в таком виде:

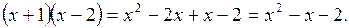
Подставим полученное выражение:

4. Вычислить интеграл

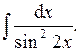
Преобразуем подынтегральную функцию таким образом:

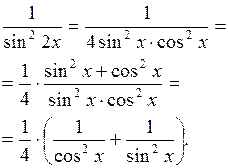
Подставляя полученную функцию, вычисляем интеграл:

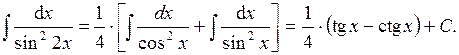
Используя правила интегрирования и таблицу интегралов, найти следующие интегралы:

4.1		4.11
4.2		4.12
4.3		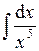4.13
4.4		4.14
4.5		4.15
4.6		4.16
4.7		4.17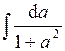
4.8		4.18
4.9		4.19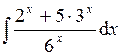
4.10		4.20