 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дифференциальное исчисление функций нескольких переменных
|
|
Задача 12. Дана функция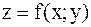 
и две точки 
и 
. Требуется: вычислить значение 
в точке В; 2) вычислить приближенное значение функции 
в точке В, исходя из значения 
функции в точке А и заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом; 4) составить уравнение касательной плоскости к поверхности 
в точке 
.
12.1. 161. 
12.2. 162. 
12.3. 163. 
12.4. 164.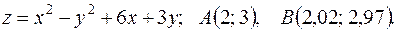 
12.5. 165. 
12.6. 166. 
12.7. 167. 
12.8. 168. 
12.9. 169. 
12.10. 170. 
Задача 13. Найти наименьшее и наибольшее значения функции z = f(x; y) в замкнутой области Д, заданной системой неравенств. Сделать чертеж.
13.1. 
.
13.2. 
.
13.3. 
.
13.4. 
.
13.5. 
.
13.6. 
13.7. 
13.8. 
.
13.9. 
.
13.10. 
.
Задача 14. Даны функция 
, точка 
и вектор 
.
Найти: 1) 
в точке А; 2) производную в точке А по направлению вектора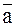 
.
14.1. 
.
14.2. 
.
14.3. 
.
14.4. 
.
14.5. 
.
14.6. 
.
14.7. 
.
14.8. 
.
14.9. 
.
14.10. 
.
Задача 15. Экспериментально получены пять значений функции 
при пяти значениях аргумента, которые записаны в таблице:
| |||||
| 
| 
| 
| 
| 
|
Методом наименьших квадратов найти функцию вида 
, выражающую приближенно (аппроксимирующую) функцию 
. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции .
15.1. 
.
15.2. 
.
15.3. 
.
15.4. 
.
15.5. 
.
15.6. 
.
15.7. 
.
15.8. 
.
15.9. 
.
15.10. 
.
Задача 16. Найти полный дифференциал функции z =f (x;y).
16.1. 
.
16.2. 
.
16.3. 
.
16.4. 
.
16.5. 
.
16.6. 
.
16.7.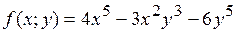 
.
16.8. 
.
16.9. 
.
16.10. 
.
Дата публикования: 2014-11-18; Прочитано: 394 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
