 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Розподіли Больцмана та Максвелла
|
|
В класичній фізиці розподіл частинок ідеального газу по енергетичним рівням в умовах термодинамічної рівноваги описується функцією Больцмана:
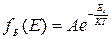 .
.
При даній Т:
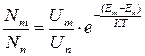 .
.
В атмосферах зірок процеси m↔n врівноважені, й зберігається іонізаційна рівновага. Концентрація атомів на будь-якому n -ому рівні визначається формулою Больцмана. Для атома водню:
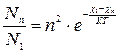 (2.18)
(2.18)
Для сонячної атмосфери при Т еф=5700К, N 2= 4,2·10-9N1 – водень майже повністю знаходиться в основному стані. Розрахунки по формулам (2.18) та (2.7) показують, що більш імовірний перехід електрона у вільний стан, ніж на збуджений рівень.
В рівноважному стані кількість частинок, що мають швидкість в інтервалі (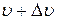 ) дається формулою Максвелла:
) дається формулою Максвелла:
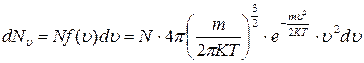 (2.19)
(2.19)
Максимуму 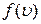 відповідає найімовірніша швидкість
відповідає найімовірніша швидкість
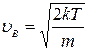 (2.20)
(2.20)
В (2.19) входить так звана кінетична температура, в (2.18) - температура збудження, в (2.4–2.7) – температура іонізації. В стані локальної термодинамічної рівноваги ці температури однакові. Якщо ж ця температура входить до (1.15), то термодинамічна рівновага є повною. Розподіл Максвела виконується для плазми в зірках головної послідовності, а також міжзоряного та міжпланетного середовищ, в котрих окремо розглядаються електронний та іонний гази з своїми температурами.
Дата публикования: 2014-11-18; Прочитано: 406 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
