Примеры решения задач. Задача 3.3.1. Конструкция состоит из двух невесомых балок, шарнирно соединенных в точке С (рис

Задача 3.3.1. Конструкция состоит из двух невесомых балок, шарнирно соединенных в точке С (рис. 3.1). Балка АС опирает­ся в точке В на шарнирно-неподвижную опору и удержи­вается на левом конце стержнем. Балка CD опи­рается правым концом на абсолютно гладкую плоскость, составляющую угол α = 60° с горизонтом. На систему дей­ствует пара сил с моментом М = 20 кНм и равномерно распределенная нагрузка с интенсивностью q = 2 кН/м. Определить реакции опор и усилие, передаваемое через шарнир. Геометрические размеры даны в метрах.

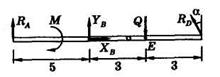
Рис. 3.1 Рис. 3.2

Решение. Если рассмотреть равновесие всей кон­струкции в целом, освободиться от связей и ввести реак­ции, учитывая, что реакция стержня направлена по стержню, реакция шарнирно-неподвижной опоры имеет неизвестное направление и ее следует разложить на составляющие по осям, а реакция при опирании тела на абсолютно гладкую плоскость пер­пендикулярна этой плоскости (нормальная реакция), то расчетная схема будет иметь вид, показанный на рис. 3.2.

Здесь распределенная нагрузка заменена сосредоточен­ной силой

.

Система сил на схеме имеет четыре неизвестных, сле­довательно, они не могут быть определены из трех уравне­ний для плоской системы сил.

Рис. 3.3

Для решения задачи расчленим конструкцию на отдель­ные тела, мысленно разделив ее по шарниру, через который передается усилие неизвестного направления (рис. 3.3).

При направлении составляющих Х_C и Y_C для левой и правой балок учтена аксиома равенства действия и противодействия. Введенные силы:

.

Уравнения для правой части:

∑X_i= 0: - X_C– R_Dsinα = 0;

∑Y_i = 0: - Y_C – Q₂ + R_D cosα = 0;

∑M_Di = 0: Y_C ∙ 4 + Q₂ ∙ 2 = 0;

Отсюда

Y_C = – 4 кН; R_D = 8 кН; X_C = – 4 кН.

Уравнения для левой части:

∑X_i = 0: X_B + X_C = 0;

∑Y_i= 0: R_A+ Y_B– Q+ Y_C= 0;

∑M_Bi= 0: - R_A∙ 5 – M– Q₁∙ 1 + Y_C∙ 2 = 0;

Отсюда

Х_B = 4 кН; R_A = – 6,4 кН; Y_B = 14,4 кН.

Для проверки правильности полученного решения мож­но составить уравнения равновесия для всей конструкции (рис. 3.2):

Задача 3.3.2. Конструкция состоит из двух тел, соединенных шарнирно в точке С. Тело АС закреплено с помощью заделки, тело ВС имеет шарнирно-подвижную опору (рис. 3.4). На тела системы действуют распределенная по линейному закону сила с максималь­ной интенсивностью q_тах = 2 кН/м, сила F = 4 кН под углом α = 30^o и пара сил с моментом М = 3 кНм. Геомет­рические размеры указаны в метрах. Определить реакции опор и усилие, пе­редаваемое через шарнир. Вес элемен­тов конструкции не учитывать.

Рис. 3.4 Рис. 3.5

Решение. Если рассмотреть рав­новесие всей конструкции в целом, учитывая, что реакция заделки состо­ит из силы неизвестного направления и пары, а реакция опоры перпендикулярна опорной поверхно­сти, то расчетная схема будет иметь вид, представленный на рис. 3.5.

Здесь равнодействующая распреде­ленной нагрузки

расположена на расстоянии двух метров (1/3 длины AD) от точки А; М_А — неизвестный момент заделки.

В данной системе сил четыре неизвестных реакции (Х_А, Y_A, M_A, R_B), и их нельзя определить из трех уравне­ний плоской системы сил.

Поэтому расчленим систему на отдельные тела по шарниру (рис. 3.6).

Рис. 3.6

Силу, приложенную в шарнире, следует при этом учи­тывать лишь на одном теле (любом из них). Уравнения для тела ВС:

Отсюда Х_С = – 1 кН; У_С = 0; R_B = 1 кН.

Уравнения для тела АС:

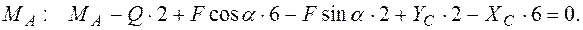
Здесь при вычислении момента силы F относительно точки А использована теорема Вариньона: сила F разло­жена на составляющие F cos α и F sin α и определена сум­ма их моментов.

Из последней системы уравнений находим:

Х_А = – 1,54 кН; У_А = 2 кН; М_А = – 10,8 кНм.

Для проверки полученного решения можно составить суммы проекций и моментов сил для всей конструкции (рис.3.5):