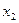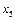|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Обработка карт
|
|
Из способа построения карты с симметричным расположением аргументов ясно, что каждая клетка функции с  аргументами имеет
аргументами имеет  соседних клеток, т.е. тех клеток, с которыми можно производить склеивание.
соседних клеток, т.е. тех клеток, с которыми можно производить склеивание.
  * *
| 
|   * *
| 
| |||
 
| 
|  * *
|

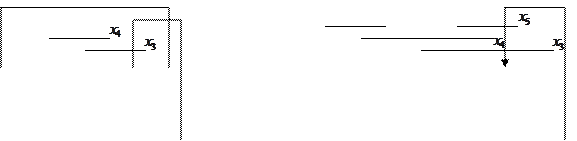 |

| 
| 
|   * *
| 
| 
| ||||||||||||

|  
|   * *
| 
| 
| 
| * | |||||||||||
 

|  * *
| 
| 

| 
| 
| * | 
| ||||||||||
| 
|
| 
| 
|   * *
|

Клетки, расположенные симметрично относительно осей, являются соседними, т.е. их можно склеить. Правило симметрии не распространяется на другие методы.
В карте проставляются только значения функции, равные 1, нули не записывают. Можно склеивать  , где
, где  , клеток, т.е. полные строки, полные столбцы, проходящие через карту, полукарту, четверть карты и т.д.
, клеток, т.е. полные строки, полные столбцы, проходящие через карту, полукарту, четверть карты и т.д.
При склеивании  клеток выпадает
клеток выпадает  переменных, т.е. останется
переменных, т.е. останется  переменных.
переменных.
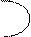
Нетрудно заметить, что простые импликанты соответствуют максимальным областям карты, т.е. таким, которые нельзя увеличить. Рассмотрим примеры.

| 
| 
| 
| |||||||||

| 
| 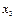
| 
|  
| 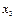
| |||||||
| 11 | 12 |  11 11
| 12 | |||||||||
 
|  13 13
| 14 |  
| 13 | 14 | |||||||
| 15 | 16 | 
| 15 |  16 16
| ||||||||

| 17 |  
| 17 | 18 | ||||||||

| 
|

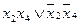

| 
| 
| 
| |||||||||

|  
| 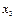
| 
|   
| 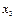
| |||||||
| 11 |  12 12
| 13 | 11 | 12 | ||||||||
 
| 14 | 15 |  
| 13 | 14 | |||||||

| 16 | 
| ||||||||||

| 17 | 18 | 19 | 
| 15 | 
| 16 | |||||

| 
|



| 
| 
| 
| |||||||||

| 
| 
| 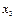
| 
| 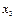
| |||||||
| 11 | 12 | 13 |   14 14
| 
| 11 | 12 | 
| 13 | ||||
 
| 15 |  16 16
| 17 |  
| 14 | |||||||

| 18 | 19 |  110 110
|  15 15
| 
| |||||||

| 111 | 112 | 
| 16 | 17 | 18 | ||||||

| 
|

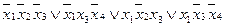
Обратите внимание, что в последней карте нет смысла объединять клетки 1, 3, 6, 8, ибо оставшиеся клетки приходится объединять с ними же.
|
|

| 
|
| 
|

| ||||||||||||||||||||

|  
| 
| 
| 
| 
| 
|  
| 
| ||||||||||||||||
 
| 
|   
| 
|  
| ||||||||||||||||||||

| 
| 
| 
| 
| ||||||||||||||||||||

| 
| |||||||||||||||||||||||

| 
|

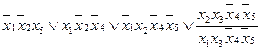
|
|

| 
|
| 
|

| ||||||||||||||||||||
 
| 
| 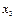
| 
|  
| 
| 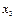
| ||||||||||||||||||

| 
| |||||||||||||||||||||||
 
|  1 1
| 
|  1 1
| 
|  
| |||||||||||||||||||

| 
| |||||||||||||||||||||||

| 
|
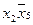
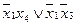

| 
|
|
|  
|  
| 
|

|
| ||||||||||||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
|  
| 
| 
| |||||||||||||||||
| 
| |||||||||||||||||||||||||||
 
|  
| 
| ||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||
 
|  
| 
| ||||||||||||||||||||||||||

| 
| 
|



|
|

| 
|
| 
|

| ||||||||||||||||||||
 
| 
| 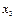
| 
| 
| 
| 
| 
| 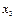
| ||||||||||||||||
 1 1
|  1 1
| 
| 
| 
| 
|  
|  1 1
| |||||||||||||||||
 
|  
| |||||||||||||||||||||||

| 
| |||||||||||||||||||||||

| 
| 
|
Дата публикования: 2014-11-18; Прочитано: 1456 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!